题目内容
11.我国古代数典籍《九章算术》“盈不足”中有一道两鼠穿墙问题:“今有垣厚十尺,两鼠对穿,初日各一尺,大鼠日自倍,小鼠日自半,问几何日相逢?”上述问题中,两鼠在第几天相逢.( )| A. | 3 | B. | 4 | C. | 5 | D. | 6、 |
分析 利用等比数列的求和公式即可得出.
解答 解:由题意可知:大老鼠每天打洞的距离是以1为首项,以2为公比的等比数列,
前n天打洞之和为$\frac{{2}^{n}-1}{2-1}$=2n-1,
同理,小老鼠每天打洞的距离$\frac{1-(\frac{1}{2})^{n}}{1-\frac{1}{2}}$=2-$\frac{1}{{2}^{n-1}}$,
∴2n-1+2-$\frac{1}{{2}^{n-1}}$=10,
解得n∈(3,4),取n=4.
即两鼠在第4天相逢.
故选:B.
点评 本题考查了等比数列的求和公式,考查了推理能力与计算能力,属于中档题.

练习册系列答案
相关题目
1.已知等差数列{an}的前n项和为Sn,且S4=6,2a3-a2=6,则a1等于( )
| A. | -3 | B. | -2 | C. | 0 | D. | 1 |
16.已知函数$f(x)=cosx+{2^x}-\frac{1}{2}(x<0)$与g(x)=cosx+log2(x+a)图象上存在关于y轴对称的点,则a的取值范围是( )
| A. | $(-∞,-\sqrt{2})$ | B. | $(-∞,-\frac{{\sqrt{2}}}{2})$ | C. | $(-\sqrt{2},\frac{{\sqrt{2}}}{2})$ | D. | $(-∞,\sqrt{2})$ |
20.圆心在直线2x-y-6=0上的圆C与y轴交于两点A(0,-5),B(0,-3),则圆C的方程是( )
| A. | (x-1)2+(y+4)2=2 | B. | (x+1)2+(y-4)2=2 | C. | (x-1)2+(y-4)2=2 | D. | (x+1)2+(y+4)2=2 |
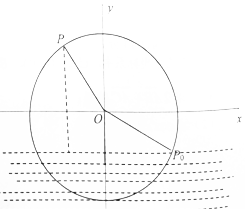 一半径为4米的水轮如图所示,水轮圆心O距离水面2米,已知水轮每60秒逆时针转动5圈,如果当水轮上点P从水中浮现时(图象P0点)开始计算时间,且点P距离水面的高度f(t)(米)与时间t(秒)满足函数:f(t)=Asin(ω+φ)+B(A>0,ω>0,|φ|<$\frac{π}{2}$).
一半径为4米的水轮如图所示,水轮圆心O距离水面2米,已知水轮每60秒逆时针转动5圈,如果当水轮上点P从水中浮现时(图象P0点)开始计算时间,且点P距离水面的高度f(t)(米)与时间t(秒)满足函数:f(t)=Asin(ω+φ)+B(A>0,ω>0,|φ|<$\frac{π}{2}$). 如图,边长为2的正方形ABCD所在平面与三角形CDE所在平面相交于CD,AE⊥平面CDE,且AE=1.
如图,边长为2的正方形ABCD所在平面与三角形CDE所在平面相交于CD,AE⊥平面CDE,且AE=1.