题目内容
已知y=kx+6k
+m在-3≤x≤0的最大值为4,最小值为-5,求k,m的值.
| 1-x |
考点:函数的最值及其几何意义
专题:数形结合,转化思想,换元法
分析:本题为利用函数单调性求解函数最值问题,难点为处理
,换元处理,转化为二次函数在闭区间上的最值问题,要注意引入新参数,转化范围.
| 1-x |
解答:
解:令
=t(由-3≤x≤0得1≤t≤2)
则x=1-t2代入换元化简得y=kt2+6kt+k+m
当k=0 时y=m,无最值,则k≠0
函数为二次函数,图象对称轴为t=-3,在t∈[1,2]上单调,有最值.
当k>0时,函数在[1,2]单调递增,得最大值为f(2)=4,最小值为f(1)=-5
即
解之得:k=1,m=-13
当k<0时,函数在[1,2]单调递减,得最大值为f(1)=4,最小值为f(2)=-5
即
解之得:k=-1,m=12
| 1-x |
则x=1-t2代入换元化简得y=kt2+6kt+k+m
当k=0 时y=m,无最值,则k≠0
函数为二次函数,图象对称轴为t=-3,在t∈[1,2]上单调,有最值.
当k>0时,函数在[1,2]单调递增,得最大值为f(2)=4,最小值为f(1)=-5
即
|
当k<0时,函数在[1,2]单调递减,得最大值为f(1)=4,最小值为f(2)=-5
即
|
点评:两个易错点,一是换元要注明引入参数的范围,二是二次函数二次项系数是否为0的讨论

练习册系列答案
相关题目
 等边△ABC的边长为1,过△ABC的中心O作OP⊥平面ABC,且OP=
等边△ABC的边长为1,过△ABC的中心O作OP⊥平面ABC,且OP=
| ||
| 3 |
| A、1 | ||||
B、
| ||||
C、
| ||||
D、
|
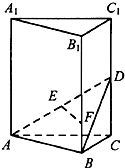 如图,在直三棱柱ABC-A1B1C1中,D、E分别为CC1、AD的中点,F为BB1上的点,且B1F=3BF
如图,在直三棱柱ABC-A1B1C1中,D、E分别为CC1、AD的中点,F为BB1上的点,且B1F=3BF