题目内容
已知函数f(x)=|x+a|+|2x-1|(a∈R).
(Ⅰ)当a=1时,求不等式f(x)≥2的解集;
(Ⅱ)若f(x)≤2x的解集包含[
,1],求a的取值范围.
(Ⅰ)当a=1时,求不等式f(x)≥2的解集;
(Ⅱ)若f(x)≤2x的解集包含[
| 1 |
| 2 |
考点:带绝对值的函数
专题:不等式的解法及应用
分析:(1)通过分类讨论,去掉绝对值函数中的绝对值符号,转化为分段函数,即可求得不等式f(x)>0的解集;
(2)由题意知,不等式可化为|x+a|+2x-1≤2x,即|x+a|≤1,解得-a-1≤x≤-a+1,
由f(x)≤2x的解集包含[
,1],可得
,解出即可得到a的取值范围.
(2)由题意知,不等式可化为|x+a|+2x-1≤2x,即|x+a|≤1,解得-a-1≤x≤-a+1,
由f(x)≤2x的解集包含[
| 1 |
| 2 |
|
解答:
解:(1)当a=1时,不等式f(x)≥2可化为|x+1|+|2x-1|≥2,
①当x≥
时,不等式为3x≥2,解得x≥
,
故此时不等式f(x)≥2的解集为x≥
;
②当-1≤x<
时,不等式为2-x≥2,解得x≤0,
故此时不等式f(x)≥2的解集为-1≤x<0;
③当x<-1时,不等式为-3x≥2,解得x≤-
,故x<-1;
综上原不等式的解集为{x|x≤0或x≥
};
(2)因为f(x)≤2x的解集包含[
,1],
不等式可化为|x+a|+2x-1≤2x,即|x+a|≤1,
解得-a-1≤x≤-a+1,
由已知得
,解得-
≤a≤0
所以a的取值范围是[-
,0].
①当x≥
| 1 |
| 2 |
| 2 |
| 3 |
故此时不等式f(x)≥2的解集为x≥
| 2 |
| 3 |
②当-1≤x<
| 1 |
| 2 |
故此时不等式f(x)≥2的解集为-1≤x<0;
③当x<-1时,不等式为-3x≥2,解得x≤-
| 2 |
| 3 |
综上原不等式的解集为{x|x≤0或x≥
| 2 |
| 3 |
(2)因为f(x)≤2x的解集包含[
| 1 |
| 2 |
不等式可化为|x+a|+2x-1≤2x,即|x+a|≤1,
解得-a-1≤x≤-a+1,
由已知得
|
| 3 |
| 2 |
所以a的取值范围是[-
| 3 |
| 2 |
点评:本题考查带绝对值的函数,考查分类讨论思想,属于中档题.

练习册系列答案
 新编小学单元自测题系列答案
新编小学单元自测题系列答案 字词句段篇系列答案
字词句段篇系列答案
相关题目
冬天是感冒传播的高发季节,连续6周中,每周患病发烧的人数如表所示,图为统计六周发烧人数的程序框图,则图中判断框,执行框应填( )

| 周次 | 1 | 2 | 3 | 4 | 5 | 6 |
| 发烧人数 | a1 | a2 | a3 | a4 | a5 | a6 |
| A、i<6;s=s+ai |
| B、i≤6;s=s+i |
| C、i≤6;s=s+ai |
| D、i>6;s=a1+a2+…+ai |
如图,该程序运行后输出的结果为( )


| A、20 | B、32 | C、38 | D、40 |
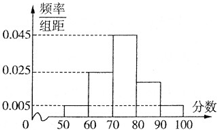 某学校举行课外综合知识比赛,随机抽取400名同学的成绩,成绩全部在50分至100分之间,将成绩按如下方式分成5组:第一组,成绩大于等于50分且小于60分;第二组,成绩大于等于60分且小于70分…第五组,成绩大于等于90分且小于等于100分,据此绘制了如图所示的频率分布直方图.则400名同学中成绩优秀(大于等于80分)的学生有
某学校举行课外综合知识比赛,随机抽取400名同学的成绩,成绩全部在50分至100分之间,将成绩按如下方式分成5组:第一组,成绩大于等于50分且小于60分;第二组,成绩大于等于60分且小于70分…第五组,成绩大于等于90分且小于等于100分,据此绘制了如图所示的频率分布直方图.则400名同学中成绩优秀(大于等于80分)的学生有