题目内容
设函数f(x)=a2x2(a>0),g(x)=blnx.
(Ⅰ)关于x的不等式(x-1)2>f(x)的解集中的整数恰有3个,求实数a的取值范围;
(Ⅱ)对于函数f(x)与g(x)定义域上的任意实数x,若存在常数k,m,使得f(x)≥kx+m和g(x)≤kx+m都成立,则称直线y=kx+m为函数f(x)与g(x)的“分界线”.设a=
,b=e,试探究f(x)与g(x)是否存在“分界线”?若存在,求出“分界线”的方程;若不存在,请说明理由.
(Ⅰ)关于x的不等式(x-1)2>f(x)的解集中的整数恰有3个,求实数a的取值范围;
(Ⅱ)对于函数f(x)与g(x)定义域上的任意实数x,若存在常数k,m,使得f(x)≥kx+m和g(x)≤kx+m都成立,则称直线y=kx+m为函数f(x)与g(x)的“分界线”.设a=
| ||
| 2 |
考点:导数在最大值、最小值问题中的应用,根的存在性及根的个数判断
专题:综合题,导数的综合应用
分析:(Ⅰ)关于由不等式解集整数的个数,然后求未知量取值范围的题目,可利用恒等变换,把它转化为求函数零点的问题,即可求解;
(Ⅱ)设F(x)=f(x)-g(x)=
x2-elnx,利用导数知识判断单调性,求出 x=
时,F(x) 取得最小值0.
设f(x)与g(x)存在“分界线”,方程为y=kx+
-k
,由 f(x)≥kx+
-k
,对x∈R恒成立,求得k=
.再利用导数证明g(x)≤
x-
(x>0)成立,从而得到所求“分界线”方程.
(Ⅱ)设F(x)=f(x)-g(x)=
| 1 |
| 2 |
| e |
设f(x)与g(x)存在“分界线”,方程为y=kx+
| e |
| 2 |
| e |
| e |
| 2 |
| e |
| e |
| e |
| e |
| 2 |
解答:
解:(Ⅰ)不等式(x-1)2>f(x)的解集中的整数恰有3个,
等价于(1-a2)x2-2x+1>0恰有三个整数解,故1-a2<0,
令h(x)=(1-a2)x2-2x+1,由h(0)=1>0且h(1)=-a2<0(a>0),
所以函数h(x)=(1-a2)x2-2x+1的一个零点在区间(0,1),
则另一个零点一定在区间(-3,-2),这是因为此时不等式解集中有-2,-1,0恰好三个整数解
故h(-2)>0,h(-3)≤0,解之得
≤a<
.
(Ⅱ)设F(x)=f(x)-g(x)=
x2-elnx,
则F′(x)=
.
所以当0<x<
时,F′(x)<0;当x<
时,F′(x)>0.
因此x=
时,F(x)取得最小值0,
则f(x)与g(x)的图象在x=
处有公共点(
,
).
设f(x)与g(x)存在“分界线”,方程为y-
=k(x-
),即y=kx+
-k
,
由f(x)≥kx+
-k
在x∈R恒成立,
则x2-2kx-e+2k
≥0在x∈R恒成立.
所以△=4(k-
)2≤0成立,
因此k=
.
下面证明g(x)≤
x-
(x>0)恒成立.
设G(x)=elnx-x
+
,则G′(x)=
.
所以当0<x<
时,G′(x)>0;当x>
时,G′(x)<0.
因此x=
时G(x)取得最大值0,则g(x)≤
x-
(x>0)成立.
故所求“分界线”方程为:y=
x-
.
等价于(1-a2)x2-2x+1>0恰有三个整数解,故1-a2<0,
令h(x)=(1-a2)x2-2x+1,由h(0)=1>0且h(1)=-a2<0(a>0),
所以函数h(x)=(1-a2)x2-2x+1的一个零点在区间(0,1),
则另一个零点一定在区间(-3,-2),这是因为此时不等式解集中有-2,-1,0恰好三个整数解
故h(-2)>0,h(-3)≤0,解之得
| 4 |
| 3 |
| 3 |
| 2 |
(Ⅱ)设F(x)=f(x)-g(x)=
| 1 |
| 2 |
则F′(x)=
(x-
| ||||
| x |
所以当0<x<
| e |
| e |
因此x=
| e |
则f(x)与g(x)的图象在x=
| e |
| e |
| e |
| 2 |
设f(x)与g(x)存在“分界线”,方程为y-
| e |
| 2 |
| e |
| e |
| 2 |
| e |
由f(x)≥kx+
| e |
| 2 |
| e |
则x2-2kx-e+2k
| e |
所以△=4(k-
| e |
因此k=
| e |
下面证明g(x)≤
| e |
| e |
| 2 |
设G(x)=elnx-x
| e |
| e |
| 2 |
| ||||
| x |
所以当0<x<
| e |
| e |
因此x=
| e |
| e |
| e |
| 2 |
故所求“分界线”方程为:y=
| e |
| e |
| 2 |
点评:本题主要考查解整式和分式不等式,导数知识判断单调性及其应用,存在性,以及探索、等价转化和推理证明能力,解决综合问题的能力.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
运行下面的程序,如果输入的n是6,那么输出的p是( )


| A、120 | B、720 |
| C、1440 | D、5040 |
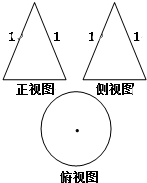 如图,一个几何体的正视图和侧视图是腰长为1的等腰三角形,俯视图是一个圆及其圆心,当这个几何体的体积最大时圆的半径是( )
如图,一个几何体的正视图和侧视图是腰长为1的等腰三角形,俯视图是一个圆及其圆心,当这个几何体的体积最大时圆的半径是( )A、
| ||||
B、
| ||||
C、
| ||||
D、
|