题目内容
已知函数f(x)=3sin(2x-
),则下列结论正确的是( )
| π |
| 4 |
| A、若f(x1)=f(x2)=0,则x1-x2=kπ(k∈Z) | ||||
B、函数f(x)的图象与g(x)=3cos(2x+
| ||||
C、函数f(x)的图象关于(-
| ||||
D、函数f(x)在区间[-
|
考点:函数y=Asin(ωx+φ)的图象变换
专题:三角函数的图像与性质
分析:由f(x1)=f(x2)=0求解x1-x2的取值集合判断A;
取x=0求对应的函数值否定B;
直接代值验证否定C;
由x的范围得到2x-
的范围判断D.
取x=0求对应的函数值否定B;
直接代值验证否定C;
由x的范围得到2x-
| π |
| 4 |
解答:
解:∵f(x)=3sin(2x-
),
若f(x1)=f(x2)=0,
则2x1-
=k1π,x1=
+
,
2x2-
=k2π,x2=
+
,
∴x1-x2=
π=
π,k∈Z.
∴选项A错误;
当x=0时,f(0)=3sin(-
)=-
,
g(0)=3cos
=
.
∴函数f(x)的图象与g(x)=3cos(2x+
)的图象不同.
∴选项B错误;
∵f(-
)=3sin[2×(-
)-
]=-3,
∴函数f(x)的图象不关于(-
,0)对称.
∴选项C错误;
当x∈[-
π,
π]时,2x-
∈[-
,
],
∴函数f(x)在区间[-
π,
π]上为增函数.
故选:D.
| π |
| 4 |
若f(x1)=f(x2)=0,
则2x1-
| π |
| 4 |
| k1π |
| 2 |
| π |
| 8 |
2x2-
| π |
| 4 |
| k2π |
| 2 |
| π |
| 8 |
∴x1-x2=
| k1-k2 |
| 2 |
| k |
| 2 |
∴选项A错误;
当x=0时,f(0)=3sin(-
| π |
| 4 |
3
| ||
| 2 |
g(0)=3cos
| π |
| 4 |
3
| ||
| 2 |
∴函数f(x)的图象与g(x)=3cos(2x+
| π |
| 4 |
∴选项B错误;
∵f(-
| π |
| 8 |
| π |
| 8 |
| π |
| 4 |
∴函数f(x)的图象不关于(-
| π |
| 8 |
∴选项C错误;
当x∈[-
| 1 |
| 8 |
| 3 |
| 8 |
| π |
| 4 |
| π |
| 2 |
| π |
| 2 |
∴函数f(x)在区间[-
| 1 |
| 8 |
| 3 |
| 8 |
故选:D.
点评:本题考查命题的真假判断与应用,考查了三角函数的图象和性质,训练了特值验证思想方法,是中档题.

练习册系列答案
相关题目
已知命题p:?x∈R,2x=1,则¬p是( )
| A、?x∉R,2x≠1 |
| B、?x∈R,2x≠1 |
| C、?x∉R,2x≠1 |
| D、?x∈R,2x≠1 |
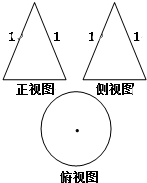 如图,一个几何体的正视图和侧视图是腰长为1的等腰三角形,俯视图是一个圆及其圆心,当这个几何体的体积最大时圆的半径是( )
如图,一个几何体的正视图和侧视图是腰长为1的等腰三角形,俯视图是一个圆及其圆心,当这个几何体的体积最大时圆的半径是( )A、
| ||||
B、
| ||||
C、
| ||||
D、
|
下列几个式子化简后的结果是纯虚数的是( )
A、
| ||
| B、(1+i)3 | ||
| C、i4 | ||
D、
|
 如图所示是根据所输入的x值计算y值的一个算法程序,若x依次取数列{
如图所示是根据所输入的x值计算y值的一个算法程序,若x依次取数列{