题目内容
20.已知a、b是异面直线,M为空间一点,M∉a,M∉b.给出下列命题:①存在一个平面α,使得b?α,a∥α;
②存在一个平面α,使得b?α,a⊥α;
③存在一条直线l,使得M∈l,l⊥a,l⊥b;
④存在一条直线l,使得M∈l,l与a、b都相交.
其中真命题的序号是①③.(请将真命题的序号全部写上)
分析 利用空间中线线、线面、面面间的关系求解.
解答 解:a、b是异面直线,M为空间一点,M∉a,M∉b,知:
①由唯一性定理得存在一个平面α,使得b?α,a∥α,故①正确;
②过b上一点作a的平行线a′,b和a′确定一个平面α,使得b?α,a∥α,故②错误;
③由两条异面直线有且只有一条公垂直线得存在一条直线l,使得M∈l,l⊥a,l⊥b,故③正确;
④点M分别与两直线a,b构成的两个平面的交线l,使得M∈l,但l与a、b不一定都相交,故④错误.
故答案为:①③.
点评 本题的考点是直线的三种位置关系和线面平行的定义,主要根据具体的位置关系和题意判断,考查了空间想象能力,是中档题.

练习册系列答案
 课前课后同步练习系列答案
课前课后同步练习系列答案 课堂小作业系列答案
课堂小作业系列答案 黄冈小状元口算速算练习册系列答案
黄冈小状元口算速算练习册系列答案 成功训练计划系列答案
成功训练计划系列答案 倍速训练法直通中考考点系列答案
倍速训练法直通中考考点系列答案 一卷搞定系列答案
一卷搞定系列答案
相关题目
15.直线ax+by-a-b=0(a≠)与圆x2+y2-2=0的位置关系为( )
| A. | 相离 | B. | 相切 | C. | 相交或相切 | D. | 相交 |
5.直线3x-y=0绕原点逆时针旋转90°,再向右平移1个单位,所得到直线的方程为( )
| A. | x+3y-3=0 | B. | x+3y-1=0 | C. | 3x-y-3=0 | D. | x-3y+3=0 |
12.如图,是圆锥一部分和四分之一球组成的组合体的三视图,则此几何体的体积为( )
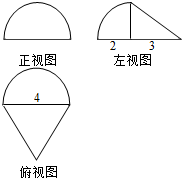

| A. | $\frac{8π}{3}$ | B. | $\frac{16π}{3}$ | C. | $\frac{14π}{3}$ | D. | $\frac{2π}{3}$ |
9.执行如图所示的程序框图,若输入的x=4.5,则输出的i=( )


| A. | 3 | B. | 4 | C. | 5 | D. | 6 |