题目内容
10.点P(x0,y0)是圆x2+y2=4上得动点,点M为OP(O是原点)的中点,则动点M的轨迹方程是x2+y2=1.分析 设OP中点M(x,y),则P(2x,2y),代入圆的方程即得线段OP中点的轨迹方程.
解答 解:设OP中点M(x,y),则P(2x,2y),代入圆的方程得(2x)2+(2y)2=4.
即x2+y2=1.
故答案为:x2+y2=1.
点评 求曲线的轨迹方程常采用的方法有直接法、定义法、相关点代入法、参数法,本题主要是利用直接法和相关点代入法,直接法是将动点满足的几何条件或者等量关系,直接坐标化,列出等式化简即得动点轨迹方程.相关点代入法 根据相关点所满足的方程,通过转换而求动点的轨迹方程.

练习册系列答案
相关题目
5.从一批产品中取出三件产品,设A={三件产品全不是次品},B={三件产品全是次品},C={三件产品至少有一件是次品},则下列结论正确的是( )
| A. | A与C互斥 | B. | A与B互为对立事件 | ||
| C. | B与C互斥 | D. | 任何两个均互斥 |
15.如图,正方体ABCD-A1B1C1D1中,点E,F分别是AA1,AD的中点,则CD1与EF所成角为( )
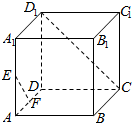

| A. | 0° | B. | 45° | C. | 60° | D. | 90° |