题目内容
10.已知椭圆$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1(a>b>0)的右焦点为F(1,0),右顶点为M($\sqrt{2}$,0).(1)求此椭圆的标准方程;
(2)设点P(2,0),点A是已知椭圆上的任意一点,点C是点A关于x轴的对称点,直线PA交椭圆于另一个不同的点B(不考虑直线PA的斜率为0的情形).问:直线BC是否一定经过右焦点F?请说明理由.
分析 (1)由右焦点和右顶点的坐标,便可求出a,b,从而得出椭圆的标准方程为$\frac{{x}^{2}}{2}+{y}^{2}=1$;
(2)可设A(x0,y0),从而有C(x0,-y0),这样即可得出直线PA的方程,而联立椭圆方程消去y便可得到$[1+\frac{2{{y}_{0}}^{2}}{({x}_{0}-2)^{2}}]{x}^{2}-\frac{8{{y}_{0}}^{2}}{({x}_{0}-2)^{2}}x+\frac{8{{y}_{0}}^{2}}{({x}_{0}-2)^{2}}-2=0$,由韦达定理即可求出xB,从而得出B点坐标,由B,C坐标即可写出直线BC方程为$\frac{x-{x}_{0}}{4-6{x}_{0}+2{{x}_{0}}^{2}}=\frac{y+{y}_{0}}{4{y}_{0}-2{x}_{0}{y}_{0}}$,令y=0便可求出x=1,从而得出直线BC一定经过右焦点F.
解答 解:(1)根据条件a=$\sqrt{2}$,c=1,∴b=1;
∴椭圆的标准方程为$\frac{{x}^{2}}{2}+{y}^{2}=1$;
(2)如图,设A(x0,y0),则C(x0,-y0);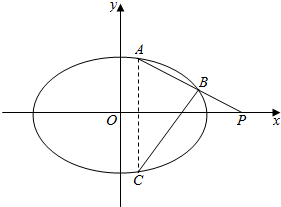
∴直线PA的斜率为$\frac{{y}_{0}}{{x}_{0}-2}$;
∴直线PA的方程为$y=\frac{{y}_{0}}{{x}_{0}-2}(x-2)$,带入椭圆方程消去y得:
$[1+\frac{2{{y}_{0}}^{2}}{({x}_{0}-2)^{2}}]{x}^{2}-\frac{8{{y}_{0}}^{2}}{({x}_{0}-2)^{2}}x+\frac{8{{y}_{0}}^{2}}{({x}_{0}-2)^{2}}-2=0$;
∴${x}_{0}{x}_{B}=\frac{\frac{8{{y}_{0}}^{2}}{({x}_{0}-2)^{2}}-2}{1+\frac{2{{y}_{0}}^{2}}{({x}_{0}-2)^{2}}}=\frac{4{x}_{0}-3{{x}_{0}}^{2}}{3-2{x}_{0}}$;
∴${x}_{B}=\frac{4-3{x}_{0}}{3-2{x}_{0}}$,带入椭圆方程$\frac{{x}^{2}}{2}+{y}^{2}=1$得:${{y}_{B}}^{2}=1-\frac{{{x}_{B}}^{2}}{2}$=$1-\frac{(\frac{4-3{x}_{0}}{3-2{x}_{0}})^{2}}{2}=\frac{2-{{x}_{0}}^{2}}{2(3-2{x}_{0})^{2}}=\frac{{{y}_{0}}^{2}}{(3-2{x}_{0})^{2}}$;
∴${y}_{B}=\frac{{y}_{0}}{3-2{x}_{0}}$;
∴$B(\frac{4-3{x}_{0}}{3-2{x}_{0}},\frac{{y}_{0}}{3-2{x}_{0}})$,又C(x0,-y0);
∴BC方程为$\frac{x-{x}_{0}}{\frac{4-3{x}_{0}}{3-2{x}_{0}}-{x}_{0}}=\frac{y+{y}_{0}}{\frac{{y}_{0}}{3-2{x}_{0}}+{y}_{0}}$;
∴$\frac{x-{x}_{0}}{4-6{x}_{0}+2{{x}_{0}}^{2}}=\frac{y+{y}_{0}}{4{y}_{0}-2{x}_{0}{y}_{0}}$,令y=0得:$\frac{x-{x}_{0}}{4-6{x}_{0}+2{{x}_{0}}^{2}}=\frac{1}{4-2{x}_{0}}$;
∴x=1;
即直线BC与x轴交点为(1,0),该点为椭圆的右焦点F;
∴直线BC一定经过右焦点F.
点评 考查椭圆的标准方程,椭圆的焦点和顶点,以及由两点求直线的斜率,直线的点斜式方程和两点式方程,韦达定理,根据直线方程求直线和x轴的交点的方法.

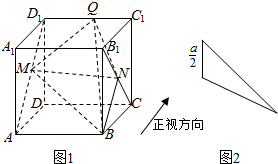
| A. | $\frac{1}{4}{a}^{2}$ | B. | $\frac{3}{4}{a}^{2}$ | C. | $\frac{1}{2}{a}^{2}$ | D. | $\frac{\sqrt{3}}{2}{a}^{2}$ |
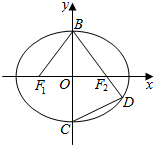 如图,在平面直角坐标系xOy中,F1,F2分别是椭圆$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1(a>b>0)的左、右焦点,B,C分别为椭圆上、下顶点,直线BF2与椭圆的另一个交点为D,若tan∠F1BO=$\frac{3}{4}$,则直线CD的斜率为$\frac{12}{25}$.
如图,在平面直角坐标系xOy中,F1,F2分别是椭圆$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1(a>b>0)的左、右焦点,B,C分别为椭圆上、下顶点,直线BF2与椭圆的另一个交点为D,若tan∠F1BO=$\frac{3}{4}$,则直线CD的斜率为$\frac{12}{25}$. 已知椭圆$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1(a>b>0)的离心率e=$\frac{\sqrt{2}}{2}$,上顶点为B(0,1).
已知椭圆$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1(a>b>0)的离心率e=$\frac{\sqrt{2}}{2}$,上顶点为B(0,1).