题目内容
18.(1)计算:$\sqrt{9}-\sqrt{2}×\root{3}{2}×\root{6}{2}$(2)已知x+x-1=3(x>0),求x${\;}^{\frac{3}{2}}$+x${\;}^{-\frac{3}{2}}$的值.
分析 (1)根据幂的运算性质计算即可,
(2)根据幂的运算性质,以及立方和公式计算即可.
解答 解:(1)原式=3-${2}^{\frac{1}{2}+\frac{1}{3}+\frac{1}{5}}$=3-2=1,
(2)∵x+x-1=3,
∴x2+x-2=7
∴(x${\;}^{\frac{3}{2}}$+x${\;}^{-\frac{3}{2}}$)2=x3+x-3+2=(x+x-1)(x2+x-2-1)+2=3×6+2=20,
∴x${\;}^{\frac{3}{2}}$+x${\;}^{-\frac{3}{2}}$=2$\sqrt{5}$
点评 本题考查了指数幂的运算性质,属于基础题.

练习册系列答案
相关题目
8.已知双曲线$\frac{{y}^{2}}{{a}^{2}}$-$\frac{{x}^{2}}{{b}^{2}}$=1(a>0,b>0)的一条渐近线平行于直线l:y=x+10,双曲线的一个焦点在直线l上,则双曲线的方程为( )
| A. | $\frac{{x}^{2}}{5}$-$\frac{{y}^{2}}{20}$=1 | B. | $\frac{{x}^{2}}{20}$-$\frac{{y}^{2}}{5}$=1 | C. | y2-x2=50 | D. | x2-y2=10 |
6.近年来我国电子商务行业迎来发展的新机遇.2016年双十一期间,某购物平台的销售业绩高达516亿人民币,与此同时,相关管理部门推出了针对电商的商品和服务的评价体系现从评价系统中选出200次成功交易,并对其评价进行统计,对商品的好评率为0.6,对服务的好评率为0.75.其中对商品和服务都做出好评的交易为80次.
(1)先完成关于商品和服务评价的2×2列联表,再判断能否在犯错误的概率不超过0.001的前提下,以为商品好评与服务好评有关?
(2)若用分层抽样的方法从“对商品好评”和“商品不满意”中抽出5次交易,再从这5次交易中选出2次,求恰有一次为“商品好评”的概率.
附临界值表:
k2的观测值:$k=\frac{{n{{(ad-bc)}^2}}}{(a+b)(c+d)(a+c)(b+d)}$,其中n=a+b+c+d
关于商品和服务评价的2×2列联表:
(1)先完成关于商品和服务评价的2×2列联表,再判断能否在犯错误的概率不超过0.001的前提下,以为商品好评与服务好评有关?
(2)若用分层抽样的方法从“对商品好评”和“商品不满意”中抽出5次交易,再从这5次交易中选出2次,求恰有一次为“商品好评”的概率.
附临界值表:
| P(k2≥k) | 0.15 | 0.10 | 0.05 | 0.025 | 0.010 | 0.005 | 0.001 |
| k | 2.072 | 2.706 | 3.841 | 5.024 | 6.635 | 7.897 | 10.828 |
关于商品和服务评价的2×2列联表:
| 对服务好评 | 对服务不满意 | 合计 | |
| 对商品好评 | a=80 | b=40 | 120 |
| 对商品不满意 | c=70 | d=10 | 80 |
13.函数f(x)=$\frac{1}{\sqrt{1-x}}$+$\sqrt{x+3}$-1的定义域是( )
| A. | (-1,3] | B. | (-1,3) | C. | [-3,1) | D. | [-3,1] |
10.设△ABC的内角A、B、C的对边分别为a、b、c,且A=60°,b=1,△ABC的面积S△ABC=$\frac{{\sqrt{3}}}{2}$,则$\frac{a+b+c}{sinA+sinB+sinC}$=( )
| A. | $\sqrt{3}$ | B. | $2\sqrt{3}$ | C. | 2 | D. | 4 |
7.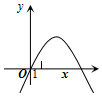 已知二次函数y=ax2+bx+c=0(a≠0)的图象如图所示,记p=|a-b+c|+|2a+b|,q=|a+b+c|+|2a-b|,则( )
已知二次函数y=ax2+bx+c=0(a≠0)的图象如图所示,记p=|a-b+c|+|2a+b|,q=|a+b+c|+|2a-b|,则( )
 已知二次函数y=ax2+bx+c=0(a≠0)的图象如图所示,记p=|a-b+c|+|2a+b|,q=|a+b+c|+|2a-b|,则( )
已知二次函数y=ax2+bx+c=0(a≠0)的图象如图所示,记p=|a-b+c|+|2a+b|,q=|a+b+c|+|2a-b|,则( )| A. | p>q | B. | p=q | ||
| C. | p<q | D. | p,q大小关系不能确定 |