题目内容
9.已知椭圆方程为$\frac{x^2}{a^2}+\frac{y^2}{b^2}=1$(a>b>0),F1,F2分别是其左、右焦点,O是坐标原点,A是椭圆上不同于顶点的任一点,$∠A{F_1}{F_2}={30^0},AO=O{F_2}$,该椭圆的离心率e=$\sqrt{3}$-1.分析 易得AF1F2是以A为直角定点的直角三角形,AF1=2a-c,AF2=c.由勾股定理得,(2a-c)2+c2=(2c)2⇒2ac+c2-a2=0⇒离心率e.
解答 解:A是椭圆上不同于顶点的任一点,$∠A{F_1}{F_2}={30^0},AO=O{F_2}$,
∴△AF1F2是以A为直角定点的直角三角形,∴AF1=2a-c,AF2=c.
由勾股定理得,(2a-c)2+c2=(2c)2⇒,2ac+c2-a2=0⇒离心率e=$\sqrt{3}-1$.
故答案为:$\sqrt{3}-1$.
点评 本题考查了椭圆的离心率,多用定义及平面几何的知识,属于基础题.

练习册系列答案
相关题目
20.已知椭圆C:$\frac{{x}^{2}}{6}$+$\frac{{y}^{2}}{9}$=1,若P(x,y)是椭圆C上一动点,则x2+y2-2x的取值范围是( )
| A. | [6-2$\sqrt{6}$,9] | B. | [6-2$\sqrt{6}$,11] | C. | [6+2$\sqrt{6}$,9] | D. | [6+2$\sqrt{6}$,11] |
17.已知P:?x∈Z,x3<1,则¬P是( )
| A. | ?x∈Z,x3≥1 | B. | ?x∉Z,x3≥1 | C. | ?x∈Z,x3≥1 | D. | ?x∉Z,x3≥1 |
4.实数2,b,a依次成等比数列,则方程$a{x^2}+bx+\frac{1}{3}=0$的实根个数为( )
| A. | 0 | B. | 1 | C. | 2 | D. | 0或2 |
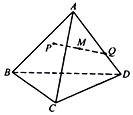 如图,在三棱锥A-BCD中,AB⊥AD,AC⊥AD,∠BAC=60°,AB=AC=AD=4,点P,Q分别在侧面ABC棱AD上运动,PQ=2,M为线段PQ中点,当P,Q运动时,点M的轨迹把三棱锥A-BCD分成上、下两部分的体积之比等于$\frac{π}{{48\sqrt{3}-π}}$.
如图,在三棱锥A-BCD中,AB⊥AD,AC⊥AD,∠BAC=60°,AB=AC=AD=4,点P,Q分别在侧面ABC棱AD上运动,PQ=2,M为线段PQ中点,当P,Q运动时,点M的轨迹把三棱锥A-BCD分成上、下两部分的体积之比等于$\frac{π}{{48\sqrt{3}-π}}$.