题目内容

7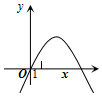．已知二次函数y=ax2+bx+c=0（a≠0）的图象如图所示，记p=|a-b+c|+|2a+b|，q=|a+b+c|+|2a-b|，则（　　）
A．p＞qB．p=q
C．p＜qD．p，q大小关系不能确定

分析 由已知可得：a＜0，$-\frac{b}{2a}＞1$，去除绝对值符号后，利用做差法，可得答案．

解答 解：∵二次函数y=ax2+bx+c=0（a≠0）的图象开口朝下，经过原点且对称轴在x=1右侧，
故a＜0，$-\frac{b}{2a}＞1$，c=0
∴2a+b＞0，2a-b＜0
又∵当x=-1时，y=a-b+c＜0，当x=1时，y=a+b+c＞0，
∴p=|a-b+c|+|2a+b|=-a+b-c+2a+b=a+2b-c，
q=|a+b+c|+|2a-b|=a+b+c-2a+b=-a+2b+c，
∴p-q=2（a-c）=2a＜0，
∴p＜q，
故选：C．

点评 本题考查的知识点是二次函数的图象和性质，熟练掌握二次函数的图象和性质，是解答的关键．

练习册系列答案
相关题目
17．已知P：?x∈Z，x3＜1，则￢P是（　　）
A．?x∈Z，x3≥1B．?x∉Z，x3≥1C．?x∈Z，x3≥1D．?x∉Z，x3≥1
18．（1）计算：$\sqrt{9}-\sqrt{2}×\root{3}{2}×\root{6}{2}$
（2）已知x+x-1=3（x＞0），求x${\;}^{\frac{3}{2}}$+x${\;}^{-\frac{3}{2}}$的值．
15．已知命题P：函数y=sin$\frac{π}{2}$x在x=a处取到最大值；命题q：直线x-y+2=0与圆（x-3）2+（y-a）2=8相切；则p是q的（　　）
A．充分不必要条件B．必要不充分条件
C．充要条件D．既不充分也不必要条件
2．设A={a}，则下列各式中正确的是（　　）
A．0∈AB．a∈AC．a⊆AD．a=A
12．判断函数 f（x）=x2 在R上的增减性．
19．某商店将进货价每个10元的商品按每个18元售出时，每天可卖出60个．商店经理到市场上做了一番调查后发现，若将这种商品的售价（在每个18元的基础上）每提高1元，则日销售量就减少5个；若将这种商品的售价（在每个18元的基础上）每降低1元，则日销售量就增加10个．为了每日获得最大利润，则此商品的售价应定为每个多少元？并求获得的最大利润．
16．若a，b，x，y∈R，则$\left\{\begin{array}{l}{x+y＞a+b}\\{（x-a）（y-b）＞0}\end{array}\right.$是$\left\{\begin{array}{l}{x＞a}\\{y＞b}\end{array}\right.$成立的必要不充分条件．（从“充分必要”，“充分不必要”，“必要不充分”，“既不充分也不必要”中选择适当的填写）
17．“a+b＜0”是“a与b均为负数的”（　　）
A．充分而不必要条件B．必要而不充分条件
C．充要条件D．既不充分又不必要条件

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网