题目内容
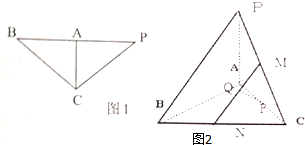 在等腰直角△BCP中,BC=PC=4,∠BCP=90°,A是边BP的中点,现沿CA把△ACP折起,使PB=4,如图1所示.
在等腰直角△BCP中,BC=PC=4,∠BCP=90°,A是边BP的中点,现沿CA把△ACP折起,使PB=4,如图1所示.(1)在三棱锥P-ABC中,求证:PA⊥平面ABC;
(2)在三棱锥P-ABC中,M,N,F分别是PC,BC,AC的中点,Q是MN上任意一点,求证:FQ∥平面PAB.
考点:直线与平面平行的判定,直线与平面垂直的判定
专题:空间位置关系与距离
分析:(1)根据线线垂直推出线面垂直;
(2)先证出面面平行再证出线面平行即可.
(2)先证出面面平行再证出线面平行即可.
解答:
解:(1)在三棱锥P-ABC中,由题意得:PA⊥AC,
∵PA=AB=2
,PB=4,∴PA2+PB2=PB2,则PA⊥AB,
又AB∩AC=A,∴PA⊥平面ABC;
(2)如图示:

∵M、N、F分别是PC、BC、AC的中点,连接FN、MF得平面FMN,
∴直线MN∥直线PB,直线FN∥直线AB,
又∵直线MN∩直线FN=你,直线PB∩直线AB=B,
∴平面PAB∥平面MNF,
又∵FQ?平面MNF,∴直线FQ∥平面PAB.
∵PA=AB=2
| 2 |
又AB∩AC=A,∴PA⊥平面ABC;
(2)如图示:

∵M、N、F分别是PC、BC、AC的中点,连接FN、MF得平面FMN,
∴直线MN∥直线PB,直线FN∥直线AB,
又∵直线MN∩直线FN=你,直线PB∩直线AB=B,
∴平面PAB∥平面MNF,
又∵FQ?平面MNF,∴直线FQ∥平面PAB.
点评:本题考查了线线垂直,线面垂直,线面平行,面面平行的性质及判定,本题属于中档题.

练习册系列答案
 鸿图图书寒假作业假期作业吉林大学出版社系列答案
鸿图图书寒假作业假期作业吉林大学出版社系列答案
相关题目
不等式组
表示的平面区域的面积为( )
|
| A、14 | B、5 | C、3 | D、7 |
已知变量x,y满足
则z=-2x+y的取值范围是( )
|
| A、(-2,2) |
| B、[-4,4] |
| C、[-2,2] |
| D、(-4,4) |
执行如图所示的程序框图,若输入n的值为8,则输出S的值为( )


| A、4 | B、6 | C、7 | D、8 |