题目内容
设变量x,y满足约束条件:
,则z=|x-3y|+5|y|的最小值为 .
|
考点:简单线性规划
专题:不等式的解法及应用
分析:作出不等式组对应的平面区域,根据区域内点的坐标将绝对值去掉,然后利用目标函数的几何意义即可得到结论.
解答:
 解:作出不等式组对应的平面区域如图:
解:作出不等式组对应的平面区域如图:
由图象知区域内的点的纵坐标y>0,且所有点都在直线x-3y=0的上方,
即区域内的点满足x-3y<0,
则z=|x-3y|+5|y|=-(x-3y)+5y=8y-x,
即y=
x+
,
平移直线y=
x+
,由图象可知当直线经过点B时,直线的截距最小,此时z也最小,
由
,解得
,即B(2,0),
此时z=|2-0|+0=2,
故答案为:2.
 解:作出不等式组对应的平面区域如图:
解:作出不等式组对应的平面区域如图:由图象知区域内的点的纵坐标y>0,且所有点都在直线x-3y=0的上方,
即区域内的点满足x-3y<0,
则z=|x-3y|+5|y|=-(x-3y)+5y=8y-x,
即y=
| 1 |
| 8 |
| z |
| 8 |
平移直线y=
| 1 |
| 8 |
| z |
| 8 |
由
|
|
此时z=|2-0|+0=2,
故答案为:2.
点评:本题主要考查线性规划的应用,根据平面区域内的点的坐标,将目标函数进行化简是解决本题的关键.

练习册系列答案
相关题目
已知向量a=(m,-2),b=(4,-2m),条件p:a∥b,条件q:m=2,则p是q的( )
| A、充分不必要条件 |
| B、必要不充分条件 |
| C、充要条件 |
| D、既不充分也不必要 |
若a是实数,则“a2≠4”是“a≠2”的( )
| A、充要条件 |
| B、既不充分也不必要条件 |
| C、充分不必要条件 |
| D、必要不充分条件 |
学校组织同学参加社会调查,某小组共有5名男同学,4名女同学.现从该小组中选出3位同学分别到A,B,C三地进行社会调查,若选出的同学中男女均有,则不同安排方法有( )
| A、70种 | B、140种 |
| C、840种 | D、420种 |
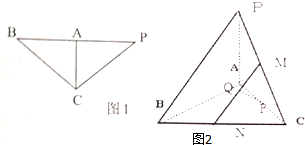 在等腰直角△BCP中,BC=PC=4,∠BCP=90°,A是边BP的中点,现沿CA把△ACP折起,使PB=4,如图1所示.
在等腰直角△BCP中,BC=PC=4,∠BCP=90°,A是边BP的中点,现沿CA把△ACP折起,使PB=4,如图1所示.