题目内容
在△ABC中,内角A、B、C所对的边分别是a,b,c,已知c=4,A=
,且函数f(x)=sinx+cosx的最大值为f(C),则△ABC的周长等于 .
| π |
| 3 |
考点:正弦定理,两角和与差的正弦函数
专题:计算题,解三角形
分析:由题意可得sin(C+
)=1,结合0<C<π,可解得C,从而可得B,由正弦定理可求得b,a的值,从而可求△ABC的周长.
| π |
| 4 |
解答:
解:∵函数f(x)=sinx+cosx=
sin(x+
)的最大值为f(C),
∴可得sin(C+
)=1,从而解得C+
=2kπ+
,k∈Z,由0<C<π,可得:C=
.从而可得:B=π-A-C=π-
-
=
,
∴由正弦定理可得:b=
=
=2
+2,a=
=
=2
.
∴△ABC的周长=a+b+c=2
+2
+2+4=6+2
+2
.
故答案为:6+2
+2
.
| 2 |
| π |
| 4 |
∴可得sin(C+
| π |
| 4 |
| π |
| 4 |
| π |
| 2 |
| π |
| 4 |
| π |
| 4 |
| π |
| 3 |
| 5π |
| 12 |
∴由正弦定理可得:b=
| csinB |
| sinC |
4×sin
| ||
sin
|
| 3 |
| csinA |
| sinC |
4×sin
| ||
sin
|
| 6 |
∴△ABC的周长=a+b+c=2
| 6 |
| 3 |
| 6 |
| 3 |
故答案为:6+2
| 6 |
| 3 |
点评:本题主要考查了正弦定理,两角和的正弦函数公式的应用,属于基本知识的考查.

练习册系列答案
 冲刺100分1号卷系列答案
冲刺100分1号卷系列答案
相关题目
学校组织同学参加社会调查,某小组共有5名男同学,4名女同学.现从该小组中选出3位同学分别到A,B,C三地进行社会调查,若选出的同学中男女均有,则不同安排方法有( )
| A、70种 | B、140种 |
| C、840种 | D、420种 |
(2-
)8展开式中各项系数的和为( )
| x |
| A、-1 | B、1 |
| C、256 | D、-256 |
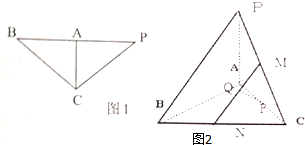 在等腰直角△BCP中,BC=PC=4,∠BCP=90°,A是边BP的中点,现沿CA把△ACP折起,使PB=4,如图1所示.
在等腰直角△BCP中,BC=PC=4,∠BCP=90°,A是边BP的中点,现沿CA把△ACP折起,使PB=4,如图1所示.