题目内容
已知α为第三象限的角，且cosα=-
，则tanα= ．
| ||
| 5 |
考点：同角三角函数基本关系的运用
专题：三角函数的求值
分析：由α为第三象限角，以及cosα的值，利用同角三角函数间的基本关系求出sinα的值，即可求出tanα的值．
解答：
解：∵α为第三象限的角，且cosα=-
，
∴sinα=-
=-
，
则tanα=
=2．
故答案为：2．
| ||
| 5 |
∴sinα=-
| 1-cos2α |
2
| ||
| 5 |
则tanα=
| sinα |
| cosα |
故答案为：2．
点评：此题考查了同角三角函数基本关系的运用，熟练掌握基本关系是解本题的关键．
练习册系列答案
相关题目
已知向量a=（m，-2），b=（4，-2m），条件p：a∥b，条件q：m=2，则p是q的（ ）
| A、充分不必要条件 |
| B、必要不充分条件 |
| C、充要条件 |
| D、既不充分也不必要 |
若a是实数，则“a2≠4”是“a≠2”的（ ）
| A、充要条件 |
| B、既不充分也不必要条件 |
| C、充分不必要条件 |
| D、必要不充分条件 |
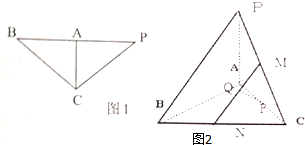在等腰直角△BCP中，BC=PC=4，∠BCP=90°，A是边BP的中点，现沿CA把△ACP折起，使PB=4，如图1所示．