题目内容
已知△ABC的三个内角A,B,C满足A>B>C,其中B=60°,且sinA-sinC+
cos(A-C)=
,则A= ,C= .
| ||
| 2 |
| ||
| 2 |
考点:三角函数中的恒等变换应用
专题:三角函数的求值,三角函数的图像与性质,解三角形
分析:直接利用三角形内角和定理求出 A+C=120°,在对三角函数关系式进行恒等变换,利用三角形的内角的大限关系,进行分类讨论,最后求出角的大小.
解答:
解:已知△ABC的三个内角A,B,C,其中B=60°,
则:A+C=120°,
所以:C=120°-A,
sinA-sinC+
cos(A-C)=
,
sinA-sin(120°-A)+
cos(2A-120°)=
,
整理得:
sinA-
cosA+
(1-2sin2(A-60°))=
,
sin(A-60°)-
sin2(A-60°)=0,
则:sin(A-60°)(1-
sin(A-60°))=0.
由于:A>B>C,
所以:0°<A-60°<60°,
则:sin(A-60°)≠0,
则:1-
sin(A-60°)=0,
由于60°<A<120°,
解得:A=105°.
利用三角形内角和定理解得:C=15°,
故答案为:A=105°,C=15°、
则:A+C=120°,
所以:C=120°-A,
sinA-sinC+
| ||
| 2 |
| ||
| 2 |
sinA-sin(120°-A)+
| ||
| 2 |
| ||
| 2 |
整理得:
| 1 |
| 2 |
| ||
| 2 |
| ||
| 2 |
| ||
| 2 |
sin(A-60°)-
| 2 |
则:sin(A-60°)(1-
| 2 |
由于:A>B>C,
所以:0°<A-60°<60°,
则:sin(A-60°)≠0,
则:1-
| 2 |
由于60°<A<120°,
解得:A=105°.
利用三角形内角和定理解得:C=15°,
故答案为:A=105°,C=15°、
点评:本题考查的知识要点:三角函数关系式的恒等变换,三角形内角和定理的应用,三角形内角的讨论及角的求法.

练习册系列答案
 核心素养学练评系列答案
核心素养学练评系列答案 单元期中期末卷系列答案
单元期中期末卷系列答案
相关题目
设x,y满足约束条件
,则z=x+3y+m的最大值为4,则m的值为( )
|
| A、-4 | B、1 | C、2 | D、4 |
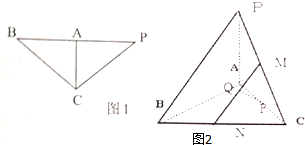 在等腰直角△BCP中,BC=PC=4,∠BCP=90°,A是边BP的中点,现沿CA把△ACP折起,使PB=4,如图1所示.
在等腰直角△BCP中,BC=PC=4,∠BCP=90°,A是边BP的中点,现沿CA把△ACP折起,使PB=4,如图1所示. 如图,在三棱柱ABC-A1B1C1中,已知AB⊥侧面BB1C1C,AB=BC=1,BB1=2,∠BCC1=60°.
如图,在三棱柱ABC-A1B1C1中,已知AB⊥侧面BB1C1C,AB=BC=1,BB1=2,∠BCC1=60°.