题目内容
已知
=(sinα,cosα),
=(-2,1),若
⊥
,则tanα的值为 .
| a |
| b |
| a |
| b |
考点:平面向量数量积的运算
专题:平面向量及应用
分析:
⊥
,可得
•
=0,再利用“弦化切”即可得出.
| a |
| b |
| a |
| b |
解答:
解:∵
⊥
,
∴
•
=-2sinα+cosα=0,
∵cosα≠0,
∴tanα=
.
故答案为:
.
| a |
| b |
∴
| a |
| b |
∵cosα≠0,
∴tanα=
| 1 |
| 2 |
故答案为:
| 1 |
| 2 |
点评:本题考查了向量垂直与数量积的关系、同角三角函数基本关系式,考查了计算能力,属于基础题.

练习册系列答案
相关题目
已知实数2、t、8构成一个等比数列,则圆锥曲线
+y2=1的离心率为( )
| x2 |
| t |
A、
| ||||||
B、
| ||||||
C、
| ||||||
D、
|
(2-
)8展开式中各项系数的和为( )
| x |
| A、-1 | B、1 |
| C、256 | D、-256 |
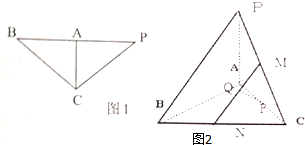 在等腰直角△BCP中,BC=PC=4,∠BCP=90°,A是边BP的中点,现沿CA把△ACP折起,使PB=4,如图1所示.
在等腰直角△BCP中,BC=PC=4,∠BCP=90°,A是边BP的中点,现沿CA把△ACP折起,使PB=4,如图1所示.