题目内容
定义在(-∞,+∞)上的任意函数f(x)都可以表示成一个奇函数g(x)和一个偶函数h(x)之和,若f(x)=ln(ex+1),那么( )
| A、g(x)=x,h(x)=ln(ex+e-x+2) | ||||
B、g(x)=
| ||||
C、g(x)=
| ||||
D、g(x)=-
|
考点:函数奇偶性的性质
专题:计算题,函数的性质及应用
分析:由题意,g(x)+h(x)=f(x)=ln(ex+1)①,g(-x)+h(-x)=f(-x)=ln(e-x+1)化简可得-g(x)+h(x)=ln(e-x+1)②,从而解出g(x)与h(x).
解答:
解:由题意,
g(x)+h(x)=f(x)=ln(ex+1)①,
g(-x)+h(-x)=f(-x)=ln(e-x+1),
即-g(x)+h(x)=ln(e-x+1)②,
①+②得
2h(x)=ln(ex+1)+ln(e-x+1)=2ln(ex+1)-x,
∴h(x)=ln(ex+1)-
,
①-②得,
g(x)=
,
故选C.
g(x)+h(x)=f(x)=ln(ex+1)①,
g(-x)+h(-x)=f(-x)=ln(e-x+1),
即-g(x)+h(x)=ln(e-x+1)②,
①+②得
2h(x)=ln(ex+1)+ln(e-x+1)=2ln(ex+1)-x,
∴h(x)=ln(ex+1)-
| x |
| 2 |
①-②得,
g(x)=
| x |
| 2 |
故选C.
点评:本题考查了奇偶性的应用,属于基础题.

练习册系列答案
相关题目
已知点A(-1,0),B(1,0),P是平面内一动点,直线PA,PB斜率之积为-
,则动点P的轨迹方程为( )
| 1 |
| 2 |
| A、2x2+y2=1(x≠±1) |
| B、x2+2y2=1(x≠±1) |
| C、x2-2y2=1(x≠±1) |
| D、2x2-y2=1(x≠±1) |
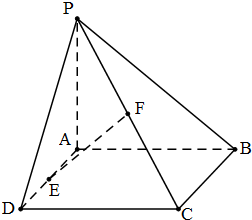 在四棱锥P-ABCD中,PA⊥面ABCD,底面ABCD为矩形,PA=AB,E、F分别为AD、PC的中点,
在四棱锥P-ABCD中,PA⊥面ABCD,底面ABCD为矩形,PA=AB,E、F分别为AD、PC的中点,