题目内容
已知等比数列{an},的前n项和为Sn,且S2=2,S4=8,则S6= .
考点:等比数列的前n项和
专题:等差数列与等比数列
分析:由等比数列的性质可得S2,S4-S2,S6-S4也成等比数列,代入数据解关于S6的方程即可.
解答:
解:由等比数列的性质可得S2,S4-S2,S6-S4也成等比数列,
∴(S4-S2)2=S2(S6-S4),代入数据可得36=2(S6-8),
解得S6=26,
故答案为:26.
∴(S4-S2)2=S2(S6-S4),代入数据可得36=2(S6-8),
解得S6=26,
故答案为:26.
点评:本题考查等比数列的性质,利用S2,S4-S2,S6-S4也成等比数列是解决问题的关键,属基础题.

练习册系列答案
相关题目
已知焦点在x轴上的椭圆离心率e=
,它的半长轴长等于圆x2+y2-2x-3=0的半径,则椭圆的标准方程是( )
| 1 |
| 2 |
A、
| ||||
B、
| ||||
C、
| ||||
D、
|
定义在(-∞,+∞)上的任意函数f(x)都可以表示成一个奇函数g(x)和一个偶函数h(x)之和,若f(x)=ln(ex+1),那么( )
| A、g(x)=x,h(x)=ln(ex+e-x+2) | ||||
B、g(x)=
| ||||
C、g(x)=
| ||||
D、g(x)=-
|
已知定义在R上的奇函数f(x),满足f(x+2)=-f(x),当c∈(0,2)时,f(x)=2x2,则f(7)=( )
| A、-2 | B、2 | C、98 | D、-98 |
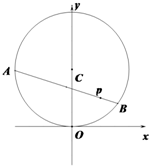 已知点P(2,2),圆C:x2+y2-8y=0,过点P的动弦AB的中点为M,O为坐标原点.
已知点P(2,2),圆C:x2+y2-8y=0,过点P的动弦AB的中点为M,O为坐标原点.