题目内容
从正方体八个点中任取两个点,在构成的所有直线中任取2条,这2条直线是异面直线的概率是 .
考点:古典概型及其概率计算公式,空间中直线与直线之间的位置关系
专题:概率与统计
分析:因为从正方体的八个顶点中任取两个点共有C82条直线,从中任意取出两条有C282种取法,从八个顶点任取四个不共面的点共有C84-12组;而其中每一组不共面的四点可出现3对异面直线.得到概率.
解答:
解:因为从正方体的八个顶点中任取两个点共有C82=28条直线,
从中任意取出两条有C282种取法,
从八个顶点任取四个不共面的点共有C84-12组;
而其中每一组不共面的四点可出现3对异面直线.
∴所求的概率为P=
=
.
故答案为:
.
从中任意取出两条有C282种取法,
从八个顶点任取四个不共面的点共有C84-12组;
而其中每一组不共面的四点可出现3对异面直线.
∴所求的概率为P=
| ||
|
| 29 |
| 63 |
故答案为:
| 29 |
| 63 |
点评:本题考查的知识点是古典概型概率计算公式,其中熟练掌握利用古典概型概率计算公式求概率的步骤,是解答的关键.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
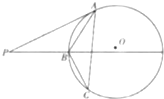 如图,过圆O外一点P分别作圆的切线和割线交圆于A,B,且PB=9,C是圆上一点使得BC=4,∠BAC=∠APB,则AB=
如图,过圆O外一点P分别作圆的切线和割线交圆于A,B,且PB=9,C是圆上一点使得BC=4,∠BAC=∠APB,则AB=