题目内容

设O为△ABC的外心（三角形外接圆的圆心）．若
AO
=
1
3
AB
+
1
3
AC
，则∠BAC的度数为（　　）
A、30°B、45°
C、60°D、90°
考点：向量加减混合运算及其几何意义
专题：平面向量及应用
分析：利用|
OA
|=|
OB
|=|
OC
|=r，运用求模运算及题干信息
AO
=
1
3
AB
+
1
3
AC
，即可求出则∠BAC
解答： 解：∵O为△ABC的外心，
∴|
OA
|=|
OB
|=|
OC
|，
又
OB
=
OA
+
AB
，
AO
=
1
3
AB
+
1
3
AC
，
∴|
OB
|2=
OA
2+
AB
2+2
OA
•
AB
，
=
OA
2+
AB
2-
2
3
(
AB
+
AC
)•
AB
，
=
OA
2+
1
3
AB
2-
2
3
AB
•
AC
，
∴
AB
•
AC
=
1
2
AB
2；
同理，
AB
•
AC
=
1
2
AC
2；
∴|
AB
|=|
AC
|，
故cos∠BAC=
AB
•
AC
|
AB
||
AC
|
=
1
2

∴∠BAC=60°，
故选：C．
点评：本题主要考察了向量的三角形法则，求模运算以及数量积的运用，属于中档题．
练习册系列答案
相关题目
给出下列命题：
①抛物线x=-
1
4
y2的准线方程是x=1；
②在进制计算中，100（2）=11（3）
③命题p：“?x∈（0，+∞），sinx+
1
sinx
≥2”是真命题；
④已知线性回归方程
y
=3+2x，当变量x增加2个单位，其预报值平均增加4个单位；
⑤设函数f（x）=
2014x+1+2013
2014x+1
+2014sinx（x∈[-
π
2
，
π
2
]）的最大值为M，最小值为m，则M+m=4027，
其中正确命题的个数是
 
个．
设[x]表示不超过实数x的最大整数，则方程[tanx]=2cos2x的解为
 
．
函数y=4x+
1
4x-5
﹙x＜
5
4
﹚在x=a时，y有最大值b，则ba=
 
．
下列有关命题的说法中错误的是（　　）
A、若“p∧q”为真命题，则p、q均为真命题．
B、若命题p“?x∈R，x2≥0”则命题￢p为“?x∈R，x2＜0”．
C、“x＞2”是“x≥0”的充分不必要条件．
D、“sinx=
1
2
”的必要不充分条件是“x=
π
6
”．
已知某算法的流程图如图所示，若输入x=7，y=6，则输出的有序数对为（　　）
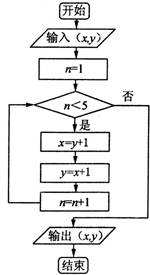
A、（13，14）
B、（12，13）
C、（14，13）
D、（13，12）
已知△ABC外接圆的半径为1，圆心为O，且
CA
+
BA
=2
OA
，|
OA
|=|
AB
|，则
CA
•
BC
的值是（　　）
A、3B、2C、-2D、-3
棱长均为3三棱锥S-ABC，若空间一点P满足
SP
=x
SA
+y
SB
+z
SC
（x+y+z=1）则|
SP
|的最小值为（　　）
A、
6
B、
6
3
C、
3
6
D、1
某校研究性学习小组，为了分析2012年某小国的宏观经济形势，查阅了有关材料，得到2011年和2012年1-5月该国CPI同比（即当年某月与前一年同月比）的增长数据（见下表），但2012年3，4，5三个月的数据（分别记为x，y，z）没有查到，有的同学清楚记得2012年1-5月的CPI数据成等差数列．
（Ⅰ）求x，y，z的值；
（Ⅱ）求2012年1-5月该国CPI数据的方差；
（Ⅲ）一般认为，某月CPI达到或超过3个百分点就已经通货膨胀，而达到或超过5个百分点则严重通货膨胀．现随机的从下表2011年的五个月和2012年的五个月的数据中各抽取一个数据，求相同月份2011年通货膨胀，并且2012年严重通货膨胀的概率．附表：2011年和2012年1-5月CPI数据（单位：百分点 注：1个百分点=1%）
年份
月份		 1 2 3 4 5
2011 2.7 2.4 2.8 3.1 2.9
2012 4.9 5.0 x y z

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网