题目内容
已知集合A={x|
≤0}，B={x||x-1|≤1}，则A∩B=（ ）
| x-1 |
| x+2 |
| A、{x|0＜x＜1} |
| B、{x|0≤x≤1} |
| C、{x|-1≤x＜0} |
| D、{x|-1＜x＜0} |
考点：交集及其运算
专题：集合
分析：根据集合的基本运算进行求解．
解答：
解：A={x|
≤0}={x|-2＜x≤1}，B={x||x-1|≤1}={x|0≤x≤2}，
则A∩B={x|0≤x≤1}，
故选：B
| x-1 |
| x+2 |
则A∩B={x|0≤x≤1}，
故选：B
点评：本题主要考查集合的基本运算，要求熟练掌握集合的交并补运算，比较基础．
练习册系列答案
相关题目
若0＜c＜1≤d，则a＜b是logcda＞logcdb成立的（ ）
| A、充分非必要条件 |
| B、必要非充分条件 |
| C、充要条件 |
| D、既不充分又不必要条件 |
设函数f（x）满足f（x+π）=f（x）+cosx，当0≤x≤π时，f（x）=0，则f（
）=（ ）
| 11π |
| 3 |
A、
| ||||
B、
| ||||
| C、0 | ||||
D、-
|
已知双曲线
-
=1的一个焦点在圆x2+y2-4x-5=0上，则双曲线的渐近线方程为（ ）
| x2 |
| 9 |
| y2 |
| m |
A、y=±
| ||||
B、y=±
| ||||
C、y=±
| ||||
D、y=±
|
一个空间几何体的三视图及尺寸大小如图所示，若侧视图为正三角形，则它的体积是（ ）A、24
| ||
B、8
| ||
C、32
| ||
D、16
|
已知点P是双曲线
-y2=1上任意一点，过点P分别作双曲线的两条渐近线的垂线，垂足分别为A、B，则
•
=（ ）
| x2 |
| 4 |
| PA |
| PB |
A、-
| ||
B、
| ||
C、-
| ||
D、-
|
已知m，n为异面直线，m?平面α，n?平面β，α∩β=l，则直线l（ ）
| A、与m，n 都相交 |
| B、至多与m，n 中的一条相交 |
| C、与m，n 都不相交 |
| D、与m，n 至少一条相交 |
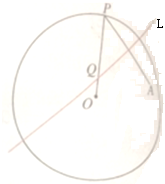如图，圆O的半径为定长r，A是圆O内一个定点，P是圆上任意一点，线段AP的垂直平分线L和半径OP相交于点Q，当点P在圆上运动时，点Q的轨迹是什么？为什么？