题目内容
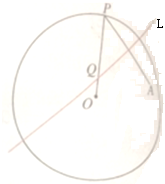如图，圆O的半径为定长r，A是圆O内一个定点，P是圆上任意一点，线段AP的垂直平分线L和半径OP相交于点Q，当点P在圆上运动时，点Q的轨迹是什么？为什么？考点：椭圆的定义
专题：圆锥曲线的定义、性质与方程
分析：由已知结合线段的垂直平分线的性质可得动点Q到两定点O、A的距离和为定值，由此可得点Q的轨迹．
解答：
解：∵A为⊙O内一定点，P为⊙O上一动点，
线段AP的垂直平分线交半径OP于点Q，
则|QA|=|QP|，则|QA|+|Q0|=|QP|+|QO|=|OP|=r，
即动点Q到两定点O、A的距离和为定值，
根据椭圆的定义，可知点Q的轨迹是：以O，A为焦点的椭圆．
线段AP的垂直平分线交半径OP于点Q，
则|QA|=|QP|，则|QA|+|Q0|=|QP|+|QO|=|OP|=r，
即动点Q到两定点O、A的距离和为定值，
根据椭圆的定义，可知点Q的轨迹是：以O，A为焦点的椭圆．
点评：本题考查了椭圆的定义及方程，考查了数学转化思想方法，是基础题．
练习册系列答案
相关题目
已知集合A={x|
≤0}，B={x||x-1|≤1}，则A∩B=（ ）
| x-1 |
| x+2 |
| A、{x|0＜x＜1} |
| B、{x|0≤x≤1} |
| C、{x|-1≤x＜0} |
| D、{x|-1＜x＜0} |
在四棱锥P-ABCD中，底面ABCD是正方形，PD⊥平面ABCD，PD=AB=2，则此四棱锥的内切球与外接球的半径分别为（ ）
A、2-
| ||||||||
B、
| ||||||||
C、，2-
| ||||||||
D、
|
一个几何体的三视图如图所示，那么该几何体的体积是（ ）
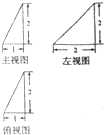
| A、3 | ||
| B、2 | ||
C、
| ||
D、
|
设 a，b，c∈R，且a＞b，则（ ）
A、
| ||||
| B、a2＞b2 | ||||
| C、a-c＞b-c | ||||
| D、ac＞bc |
