题目内容
已知正项等比数列{an}满足:a7=a6+2a5,若存在两项am,an,使得aman=16a12,则
+
的最小值为( )
| 1 |
| m |
| 4 |
| n |
A、
| ||
B、
| ||
C、
| ||
| D、不存在 |
考点:基本不等式,等比数列的通项公式
专题:常规题型,高考数学专题
分析:应先从等比数列入手,利用通项公式求出公比q,然后代入到aman=16a12中,可得到关于m,n的关系式,再利用基本不等式的知识解决问题.
解答:
解:设正项等比数列{an}的公比为q,易知q≠1,由a7=a6+2a5,得到a6q=a6+2
,解得q=-1或q=2,
因为{an}是正项等比数列,所以q>0,因此,q=-1舍弃.
所以,q=2
因为aman=16a12,所以a12m-1a12n-1=16a12,所以m+n=6,(m>0,n>0),
所以
+
=
(m+n)(
+
)=
(5+
+
)≥
(5+2
)=
,
当且仅当
=
,且m+n=6,即m=2,n=4时等号成立.
故选A
| a6 |
| q |
因为{an}是正项等比数列,所以q>0,因此,q=-1舍弃.
所以,q=2
因为aman=16a12,所以a12m-1a12n-1=16a12,所以m+n=6,(m>0,n>0),
所以
| 1 |
| m |
| 4 |
| n |
| 1 |
| 6 |
| 1 |
| m |
| 4 |
| n |
| 1 |
| 6 |
| n |
| m |
| 4m |
| n |
| 1 |
| 6 |
|
| 3 |
| 2 |
当且仅当
| n |
| m |
| 4m |
| n |
故选A
点评:对等比数列的考查一定要突出基本量思想,常规思路一般利用同项、求和公式,利用首项,公比表示已知,进一步推出我们需要的隐含条件或结论;基本不等式要重视其适用条件的判断,这里容易在取“=”时出错.

练习册系列答案
 轻松暑假总复习系列答案
轻松暑假总复习系列答案
相关题目
抛物线C1:y=ax2(a>0)的焦点与双曲线C2:
-y2=1的右焦点的连线交C1于第一象限的点M,若C1在点M处的切线平行于C2的一条渐近线,则a=( )
| x2 |
| 3 |
A、
| ||||
B、
| ||||
C、
| ||||
D、
|
已知弹簧的一端固定在地面上,另一端固定一个小球,已知小球在达到平衡位置之前处于加速状态,且加速度与时间的函数关系为a(t)=2t+
+3,则当t=1时小球的速度为( )
| 10 |
| 1+t |
| A、4+10ln2 |
| B、5+10ln2 |
| C、4-10ln2 |
| D、5-10ln2 |
已知复数z=(x2-1)+(x+1)i(x∈R,i是虚数单位)是纯虚数,则x的值为( )
| A、-1 | B、1 | C、±1 | D、0 |
已知集合A={-2,-1,1,2},B={x|x2-x-2≥0},则A∩(∁RB)=( )
| A、{1} |
| B、{-1,1} |
| C、{-2,1,2} |
| D、{-2,-1,1} |
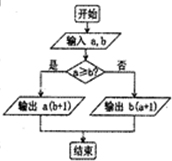 如图,定义某种运算S=a?b,运算原理如图所示,则式子(2tan
如图,定义某种运算S=a?b,运算原理如图所示,则式子(2tan