题目内容
设抛物线x2=8y的焦点为F，准线为l，P为抛物线上一点，PA⊥l，A为垂足，如果直线AF的倾斜角等于60°，那么|PF|等于（ ）
A、2
| ||
B、4
| ||
C、
| ||
| D、4 |
考点：抛物线的简单性质
专题：计算题,圆锥曲线的定义、性质与方程
分析：先求出|AF|，过P作PB⊥AF于B，利用|PF|=
，求出|PF|．
| |BF| |
| cos30° |
解答：
解：在△APF中，由抛物线的定义，可得|PA|=|PF|，
∵|AF|sin 60°=4，∴|AF|=
，
又∠PAF=∠PFA=30°，过P作PB⊥AF于B，则|PF|=
=
．
故选：C．
解：在△APF中，由抛物线的定义，可得|PA|=|PF|，∵|AF|sin 60°=4，∴|AF|=
| 8 | ||
|
又∠PAF=∠PFA=30°，过P作PB⊥AF于B，则|PF|=
| |BF| |
| cos30° |
| 8 |
| 3 |
故选：C．
点评：抛物线的定义，可以将抛物线上的点到焦点的距离转化为到准线的距离．
练习册系列答案
名校课堂系列答案
相关题目
从某班50名学生的一次数学测试成绩进行调查，发现其成绩都在90到150之间，频率分布直方图如图所示．程序框图的运算结果为（ ）
| A、12 | B、24 | C、16 | D、48 |
已知正项等比数列{an}满足：a7=a6+2a5，若存在两项am，an，使得aman=16a12，则
+
的最小值为（ ）
| 1 |
| m |
| 4 |
| n |
A、
| ||
B、
| ||
C、
| ||
| D、不存在 |
已知角φ的终边经过点P（3，-4），函数f（x）=sin（ωx+φ）（ω＞0）的图象的相邻的两条对称轴之间的距离等于
，则f（
）的值为（ ）
| π |
| 3 |
| π |
| 12 |
A、
| ||||
B、-
| ||||
C、
| ||||
D、-
|
正方体ABCD-A1B1C1D1的8个顶点中任取4个连接构成的三棱锥中，满足任意一条棱都不与其表面垂直的三棱锥的个数（ ）| A、22 | B、24 | C、26 | D、28 |
已知函数f（x）=
，则f（f（2014））=（ ）
|
A、
| ||
B、-
| ||
| C、1 | ||
| D、-1 |
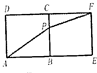一同学为研究函数f（x）=