题目内容
已知实系数方程x2+ax+1=0的一个实根在区间(1,2)内,则a的取值范围是 .
考点:一元二次方程的根的分布与系数的关系
专题:函数的性质及应用
分析:设函数f(x)=x2+ax+1,利用根与系数之间的关系,建立条件关系即可得到结论.
解答:
解:设f(x)=x2+ax+1,
∵f(0)=1>0,方程x2+ax+1=0的一个实根在区间(1,2)内,
∴
或
,
即
①或
②,
由①得无解,由②得-
<a<-2,
故答案为:(-
,-2).
∵f(0)=1>0,方程x2+ax+1=0的一个实根在区间(1,2)内,
∴
|
|
即
|
|
由①得无解,由②得-
| 5 |
| 2 |
故答案为:(-
| 5 |
| 2 |
点评:本题主要考查二次函数和二次方程之间的关系,将方程转化为函数是解决本题的关键.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
已知正项等比数列{an}满足:a7=a6+2a5,若存在两项am,an,使得aman=16a12,则
+
的最小值为( )
| 1 |
| m |
| 4 |
| n |
A、
| ||
B、
| ||
C、
| ||
| D、不存在 |
若x,y满足约束条件
,则
的最小值为( )
|
| x |
| y |
A、
| ||
B、
| ||
| C、1 | ||
D、
|
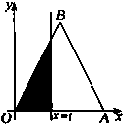 如图,△OAB是边长为2的正三角形,记△OAB位于直线x=t(0<t≤2)左侧的图形的面积为f(t),则
如图,△OAB是边长为2的正三角形,记△OAB位于直线x=t(0<t≤2)左侧的图形的面积为f(t),则 从某班50名学生的一次数学测试成绩进行调查,发现其成绩都在90到150之间,频率分布直方图如图所示.
从某班50名学生的一次数学测试成绩进行调查,发现其成绩都在90到150之间,频率分布直方图如图所示.