题目内容

某四棱锥的三视图如图所示，则该四棱锥的四个侧面面积中，最大的面积值为
 
．
考点：由三视图求面积、体积
专题：计算题,空间位置关系与距离
分析：三视图中长对正，高对齐，宽相等；由三视图想象出直观图，一般需从俯视图构建直观图．
解答： 解：由题意，该四棱锥的四个侧面面积中，较大的两个面的面积分别为
S1=
1
2
×4×
42+32
=10，
S2=
1
2
×3×
42+42
=6
2
，
6
2
＜10，
故答案为：10．
点评：三视图中长对正，高对齐，宽相等；由三视图想象出直观图，一般需从俯视图构建直观图，本题考查了学生的空间想象力，识图能力及计算能力．
练习册系列答案
相关题目
如图所示，使用模拟方法估计圆周率值的程序框图，P表示估计的结果，则图中空白框内应填入P=（　　）
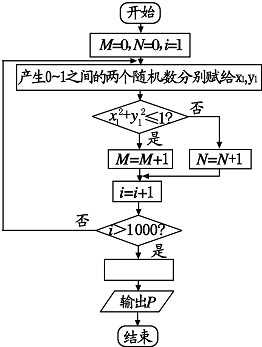
A、
M
1000
B、
1000
M
C、
4M
1000
D、
1000
4M
坛子中有6个阄，其中3个标记为“中奖”，另外三个标记是“谢谢参与”，甲、乙、丙三人份两轮按甲、乙、丙、甲、乙、丙的顺序依次抽取，当有人摸到“中奖”阄时，摸奖随即结束．
（1）若按有放回抽取，甲、乙、丙的中奖概率分别是多少？
（2）若按不放回抽取，甲、乙、丙的中奖概率分别是多少？
（3）按不放回抽取，第一轮摸奖时有人中奖则可获得奖金10000元，第二轮摸奖时才中奖可获得奖金6000元，求甲、乙、丙三人所获奖金总额ξ的分布列和数学期望．
已知函数f（x）=
2x+a，x＜2
-x-2a，x≥2
，若f（2-a）=f（2+a），则a的值为
 
．
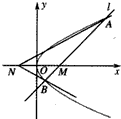已知过点M（a，0）（a＞0）的动直线l交抛物线y2=4x于A、B两点，点N与点M关于y轴对称，
（1）当a=1时，求证：∠ANM=∠BNM；
（2）对于给定的正数a，是否存在直线l′：x=m，使得l′被以AM为直径的圆所截得的弦长为定值？如果存在，求出直线l′的方程，如果不存在，试说明理由．
如果实数x，y满足：
x-y+1≤0
x+y-2≤0
x+1≥0
，则目标函数z=4x+y的最大值为（　　）
A、2
B、3
C、
7
2
D、4
对于函数f（x）定义域内的任意x1，x2（x1≠x2），有以下结论：
①f（0）=1； 
②f（x1+x2）=f（x1）•（x2）； 
③f（x1•x2）=f（x1）+（x2）；
④
f(x1)-f(x2)
x1-x2
＞0； 
⑤f（
x1+x2
2
）＜
f(x1)+f(x2)
2
．
当f（x）=lgx时，上述结论中，正确的是
 
（填入你认为正确的所有结论的序号）
设集合A={1，3，x}，集合B={3，7，11}，对任意x∈A，f：x→2x+1表示从集合A到集合B的函数，则实数x的值为
 
．
已知函数f（x）=x2-2ax+1，且函数f（x）在（-∞，-1]上是单调递减函数，在[1，+∞）上是单调递增函数．
（1）求实数a的取值集合A；
（2）设函数g（x）=-x2-x+
3
4
，若对任意a∈A及t∈[-1，1]都有不等式m2+2tm+1≥g（a）成立，求实数m的取值范围．

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网