��Ŀ����
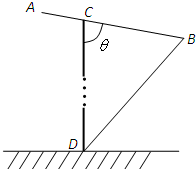 ij����װ����ͼ��ʾ�����иֽṹABD��AB=BD=l����B=
ij����װ����ͼ��ʾ�����иֽṹABD��AB=BD=l����B=| �� |
| 3 |
��1�����ȱ仯ʱ���Խ��������е�ʱ��t��ʾ�ɦȵĺ������ú���v��l��ʽ�ӣ���
��2����t��Сʱ��C��Ӧ�����AB��ʲôλ�ã�
���㣺��֪���Ǻ���ģ�͵�Ӧ������,���ϵĺ���,��������ʽ����⼰���÷���,���Ǻ�������ֵ
ר�⣺Ӧ����,��������
�������ڣ�1���ʣ�ʱ��t�ֳ����Σ���D��C��Ϊt1����C��A��Ϊt2��Ҫ����t��ȵĺ�����ϵ����Ҫ���������Σ����������Ҷ���������ڣ�2���ʣ����ݵڣ�1�������Ǻ�������ʽ������=
ʱ��tȡ��Сֵ��
| �� |
| 2 |
���
 �⣺��1����ͼ������AD���ڡ�ACD�У�AB=BD=l����B=
�⣺��1����ͼ������AD���ڡ�ACD�У�AB=BD=l����B=
��
��AD=l����A�T
��
�����D����C�������ٶ�Ϊv�������е�ʱ��Ϊt1����CD=vt1��
�����C����A�������ٶ�Ϊ3v�������е�ʱ��Ϊt2����AC=3vt2��
���ڡ�ACD�У������Ҷ����ã�
=
��
=
��t1=
��t2=
��t=t1+t2=
+
=
����
���ȣ�
����
��2���ɣ�1��֪����=
��t��С����C��AB���е�ʱ��tȡ��Сֵ��
 �⣺��1����ͼ������AD���ڡ�ACD�У�AB=BD=l����B=
�⣺��1����ͼ������AD���ڡ�ACD�У�AB=BD=l����B=| �� |
| 3 |
��AD=l����A�T
| �� |
| 3 |
�����D����C�������ٶ�Ϊv�������е�ʱ��Ϊt1����CD=vt1��
�����C����A�������ٶ�Ϊ3v�������е�ʱ��Ϊt2����AC=3vt2��
���ڡ�ACD�У������Ҷ����ã�
| vt1 |
| sinA |
| l |
| sin(��-��) |
| 3vt2 | ||
sin(��-
|
| l |
| sin(��-��) |
��t1=
| ||
| 2vsin�� |
lsin(��-
| ||
| 3vsin�� |
��t=t1+t2=
| ||
| 2vsin�� |
lsin(��-
| ||
| 3vsin�� |
=
3
| ||||
| 6vsin�� |
| �� |
| 3 |
| 2�� |
| 3 |
��2���ɣ�1��֪����=
| �� |
| 2 |
���������⿼�������⺯������������֪ʶ���ۺ�Ӧ�ã��ѶȽϴؼ���ͨ���������������������Ҷ����������Ǻ���ģ�ͣ�

��ϰ��ϵ�д�
�����Ŀ
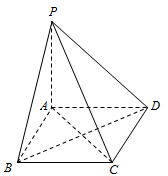 ��ͼ����P-ABCD�ĵ���ABCD�Ǿ��Σ�PA��ƽ��ABCD��PA=AD=2��BD=2
��ͼ����P-ABCD�ĵ���ABCD�Ǿ��Σ�PA��ƽ��ABCD��PA=AD=2��BD=2