题目内容
设二次函数f(x)=ax2+bx+c(a≠0),且方程f(x)=x有两相等的实数根1.
(1)若f(0)=2,求f(x)的解析式;
(2)求f(x)在[-2,2]的最小值(用a表示).
(1)若f(0)=2,求f(x)的解析式;
(2)求f(x)在[-2,2]的最小值(用a表示).
考点:二次函数的性质,二次函数在闭区间上的最值
专题:函数的性质及应用
分析:(1)由韦达定理得出方程组,解出a,b,c的值即可;(2)先找出函数的对称轴通过讨论a的取值范围综合得出结论.
解答:
解:(1)若方程f(x)=x有两相等的实数根1,
∴ax2+(b-1)x+c=0,
于是可得
,
故
,
又f(0)=2,
故c=2,
∴a=2,b=-3
∴f(x)=2x2-3x+2.
(2)∵f(x)=ax2+(1-2a)x+a,
∴对称轴x=1-
,
当a<0时,二次函数的图象开口向下,
f(-2)=9a-2,f(2)=a+2,
f(-2)-f(2)=8a-4<0,
∴f(x)min=f(-2)=9a-2;
当a>0时,1-
<2,
又∵二次函数的图象开口向上,
故当1-
<-2时,
即0<a<
时,f(x)在[-2,2]递增;
∴f(x)min=f(-2)=9a-2,
当-2<1-
<2,f(x)min=f(1-
)=1-
,
综上所述∴f(x)min=
.
∴ax2+(b-1)x+c=0,
于是可得
|
故
|
又f(0)=2,
故c=2,
∴a=2,b=-3
∴f(x)=2x2-3x+2.
(2)∵f(x)=ax2+(1-2a)x+a,
∴对称轴x=1-
| 1 |
| 2a |
当a<0时,二次函数的图象开口向下,
f(-2)=9a-2,f(2)=a+2,
f(-2)-f(2)=8a-4<0,
∴f(x)min=f(-2)=9a-2;
当a>0时,1-
| 1 |
| 2a |
又∵二次函数的图象开口向上,
故当1-
| 1 |
| 2a |
即0<a<
| 1 |
| 6 |
∴f(x)min=f(-2)=9a-2,
当-2<1-
| 1 |
| 2a |
| 1 |
| 2a |
| 1 |
| 4a |
综上所述∴f(x)min=
|
点评:本题考察了二次函数的性质问题,求函数的解析式问题,求函数在闭区间上的最值问题,渗透了分类讨论思想,是一道中档题.

练习册系列答案
 期末1卷素质教育评估卷系列答案
期末1卷素质教育评估卷系列答案
相关题目
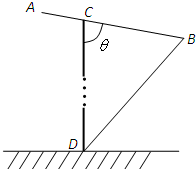 某运输装置如图所示,其中钢结构ABD是AB=BD=l,∠B=
某运输装置如图所示,其中钢结构ABD是AB=BD=l,∠B=