题目内容
在△ABC中,内角A,B,C的对边分别为a,b,c,若3a=5b,且sinA是sinB与sinC的等差中项,则角C= .
考点:余弦定理,正弦定理
专题:三角函数的求值
分析:在△ABC中,由3a=5b利用正弦定理可得3sinA=5sinB,再由sinB+sinC=2sinA求得sinC=
sinB,可得c=
b.再由余弦定理可得cosC=
的值,可得角C的值.
| 7 |
| 3 |
| 7 |
| 3 |
| a2+b2-c2 |
| 2ab |
解答:
解:在△ABC中,∵3a=5b,故由正弦定理可得3sinA=5sinB.
再由sinA是sinB与sinC的等差中项,可得sinB+sinC=2sinA.
故有 sinC=
sinB,∴c=
b.
再由余弦定理可得cosC=
=
=-
,则角C=120°,
故答案为:120°.
再由sinA是sinB与sinC的等差中项,可得sinB+sinC=2sinA.
故有 sinC=
| 7 |
| 3 |
| 7 |
| 3 |
再由余弦定理可得cosC=
| a2+b2-c2 |
| 2ab |
| ||||
2×
|
| 1 |
| 2 |
故答案为:120°.
点评:本题主要考查等差中项的定义,正弦定理、余弦定理的应用,根据三角函数的值求角,属于中档题.

练习册系列答案
 黄冈创优卷系列答案
黄冈创优卷系列答案
相关题目
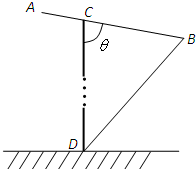 某运输装置如图所示,其中钢结构ABD是AB=BD=l,∠B=
某运输装置如图所示,其中钢结构ABD是AB=BD=l,∠B=