题目内容
已知f(x)满足f(0)=1,f(x+1)-f(x)=2x,
(1)求二次函数f(x)的解析式;
(2)若不等式f(x)>2x+m在[-1,1]上恒成立,求实数m的取值范围.
(1)求二次函数f(x)的解析式;
(2)若不等式f(x)>2x+m在[-1,1]上恒成立,求实数m的取值范围.
考点:二次函数的性质,二次函数在闭区间上的最值
专题:函数的性质及应用
分析:(1)设出函数f(x)的解析式,分别由f(0)=1,f(x+1)-f(x)=2x,求出a,b,c的值;
(2)将不等式变形为m<x2-3x+1的形式,求出x2-3x+1在区间[-1,1]上的最小值即可.
(2)将不等式变形为m<x2-3x+1的形式,求出x2-3x+1在区间[-1,1]上的最小值即可.
解答:
解:(1)设f(x)=ax2+bx+c
由f(0)=1,得c=1,
由f(x+1)-f(x)=2x得:
a(x+1)2+b(x+1)+1-ax2-bx-1=2x,
化简,解得:a=1,b=-1,
∴f(x)=x2-x+1.
(2)由题f(x)=x2-x+1>2x+m在[-1,1]上恒成立,
即m<x2-3x+1,x∈[-1,1],
令y=x2-3x+1,对称轴x=
,
∴函数y=x2-3x+1在[-1,1]单调递减,
则m<(x2-3x+1)min=-1,
∴m<-1.
由f(0)=1,得c=1,
由f(x+1)-f(x)=2x得:
a(x+1)2+b(x+1)+1-ax2-bx-1=2x,
化简,解得:a=1,b=-1,
∴f(x)=x2-x+1.
(2)由题f(x)=x2-x+1>2x+m在[-1,1]上恒成立,
即m<x2-3x+1,x∈[-1,1],
令y=x2-3x+1,对称轴x=
| 3 |
| 2 |
∴函数y=x2-3x+1在[-1,1]单调递减,
则m<(x2-3x+1)min=-1,
∴m<-1.
点评:本题考察了二次函数的性质,求二次函数的解析式以及二次函数在闭区间上的最值问题,本题是一道基础题.

练习册系列答案
 金博士一点全通系列答案
金博士一点全通系列答案
相关题目
 如图,已知三棱柱ABC-A1B1C1的侧棱与底面垂直,AA1=AB=AC=1,AB⊥AC,M是CC1的中点,N是BC的中点,点P在直线A1B1上,且满足
如图,已知三棱柱ABC-A1B1C1的侧棱与底面垂直,AA1=AB=AC=1,AB⊥AC,M是CC1的中点,N是BC的中点,点P在直线A1B1上,且满足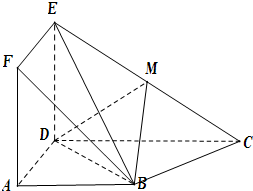 如图,正方形ADEF与梯形ABCD所在平面互相垂直,AD⊥CD,AB∥CD,AB=AD=
如图,正方形ADEF与梯形ABCD所在平面互相垂直,AD⊥CD,AB∥CD,AB=AD=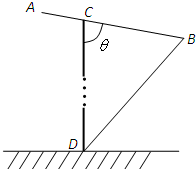 某运输装置如图所示,其中钢结构ABD是AB=BD=l,∠B=
某运输装置如图所示,其中钢结构ABD是AB=BD=l,∠B=