题目内容
已知函数y=f(x)的图象在点M(1,f(x))处的切线方程是y=
x+2,
(1)求f(1)+f′(1)的值.
(2)求函数y=(2x-1)3的导数.
| 1 |
| 2 |
(1)求f(1)+f′(1)的值.
(2)求函数y=(2x-1)3的导数.
考点:利用导数研究曲线上某点切线方程,简单复合函数的导数
专题:计算题,导数的概念及应用
分析:(1)根据切点在直线上,求出f(1),由导数的几何意义得f′(1),再相加即可;
(2)可以写成(2x-1)(2x-1)2,再由导数的乘法法则即可求出,或者运用复合函数的求导法则得到.
(2)可以写成(2x-1)(2x-1)2,再由导数的乘法法则即可求出,或者运用复合函数的求导法则得到.
解答:
解:(1)∵函数y=f(x)的图象在点M(1,f(x))处的切线方程是y=
x+2,
∴f(1)=
+2=
,f′(1)=
,
∴f(1)+f′(1)=
+
=3;
(2)∵函数y=(2x-1)3的导数,
∴y′=2(2x-1)2+(2x-1)(8x-4)=6(2x-1)2,
或运用复合函数的求导法则,
得到导数y′=3(2x-1)2•2=6(2x-1)2.
| 1 |
| 2 |
∴f(1)=
| 1 |
| 2 |
| 5 |
| 2 |
| 1 |
| 2 |
∴f(1)+f′(1)=
| 5 |
| 2 |
| 1 |
| 2 |
(2)∵函数y=(2x-1)3的导数,
∴y′=2(2x-1)2+(2x-1)(8x-4)=6(2x-1)2,
或运用复合函数的求导法则,
得到导数y′=3(2x-1)2•2=6(2x-1)2.
点评:本题主要考查导数与切线方程之间的关系,考查导数的运算法则和求导公式,是一道基础题.

练习册系列答案
相关题目
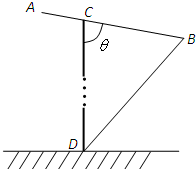 某运输装置如图所示,其中钢结构ABD是AB=BD=l,∠B=
某运输装置如图所示,其中钢结构ABD是AB=BD=l,∠B=