题目内容
抛物线y=
（x-2）2的图象可由抛物线y=
x2向 平移 个单位得到，它的顶点坐标是 ，对称轴是 ．
| 1 |
| 3 |
| 1 |
| 3 |
考点：函数的图象与图象变化
专题：函数的性质及应用
分析：根据函数图象平移变换“左加右减，上加下减”的法则，和平移前后的函数解析式，可得平移方式，再由二次函数的图象和性质得到其图象顶点坐标和对称轴方程．
解答：
解：根据函数图象平移变换“左加右减，上加下减”的法则，
抛物线y=
x2向右平移2个单位可得抛物线y=
（x-2）2的图象，
其顶点坐标为（2，0），对称轴方程为：直线x=2，
故答案为：右，2，（2，0），x=2
抛物线y=
| 1 |
| 3 |
| 1 |
| 3 |
其顶点坐标为（2，0），对称轴方程为：直线x=2，
故答案为：右，2，（2，0），x=2
点评：本题考查的知识点是函数图象的平移变换法则，二次函数的图象和性质，难度不大，属于基础题．
练习册系列答案
鸿图图书寒假作业假期作业吉林大学出版社系列答案
相关题目
如图为一半径为2的扇形（其中扇形中心角为90°），在其内部随机地撒一粒黄豆，则它落在阴影部分的概率为（ ）A、
| ||
B、
| ||
C、
| ||
D、1-
|
已知三点A（1，1），B（-1，0），C（0，1），若
和
是相反向量，则点D的坐标是（ ）
| AB |
| CD |
| A、（-2，0） |
| B、（2，2） |
| C、（2，0） |
| D、（-2，-2） |
某城市为保护环境，维护水资源，鼓励市民家庭节约用水，作出了如下规定：每月用水不超过4吨，按每吨2元收取消费；每月超过4吨，超过部分加倍收费，某市民家庭某月缴费20元，则该市民家庭这个月实际用水（ ）
| A、7吨 | B、8吨 | C、9吨 | D、10吨 |
函数y=x3+
是（ ）
| 1 |
| x |
| A、奇函数 | B、偶函数 |
| C、既奇又偶函数 | D、非奇非偶函数 |
函数f（x）=log2|x-1|的图象大致是（ ）
A、 |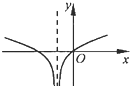
B、 |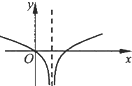
C、 |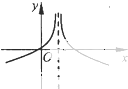
D、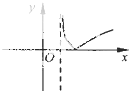 |