题目内容
在数列{an}中,a1=1,an=
(an-1+
)(n≥2),试猜想这个数列的通项公式为( )
| 1 |
| 2 |
| 1 |
| an-1 |
A、an=
| ||||
B、an=
| ||||
| C、an=n | ||||
| D、an=1 |
考点:归纳推理
专题:推理和证明
分析:由已知中a1=1,an=
(an-1+
)(n≥2),逐一求出an的值,归纳推理可得数列的通项公式.
| 1 |
| 2 |
| 1 |
| an-1 |
解答:
解:∵a1=1,an=
(an-1+
)(n≥2),
∴a2=
(a1+
)=
(1+1)=1,
a3=
(a2+
)=
(1+1)=1,
a4=
(a3+
)=
(1+1)=1,
…
由此猜想an=1.
用数学归纳法证明:
①当n=1时,a1=1,成立;
②假设n=k时,ak=1成立,
当n=k+1时,ak+1=
(ak+
)=
(1+1)=1,也成立.
由①②,知an=1.
故选:D
| 1 |
| 2 |
| 1 |
| an-1 |
∴a2=
| 1 |
| 2 |
| 1 |
| a1 |
| 1 |
| 2 |
a3=
| 1 |
| 2 |
| 1 |
| a2 |
| 1 |
| 2 |
a4=
| 1 |
| 2 |
| 1 |
| a3 |
| 1 |
| 2 |
…
由此猜想an=1.
用数学归纳法证明:
①当n=1时,a1=1,成立;
②假设n=k时,ak=1成立,
当n=k+1时,ak+1=
| 1 |
| 2 |
| 1 |
| ak |
| 1 |
| 2 |
由①②,知an=1.
故选:D
点评:本题考查数列的通项公式的求法,是基础题.解题时要认真审题,注意递推公式和数学归纳法的合理运用.

练习册系列答案
相关题目
已知a=0.80.8,b=0.80.9,c=1.20.8,则a,b,c三者的大小关系是( )
| A、b<a<c |
| B、b<c<a |
| C、a<b<c |
| D、c<b<a |
函数f(x)=log2|x-1|的图象大致是( )
A、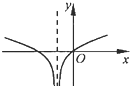 |
B、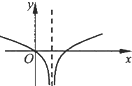 |
C、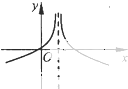 |
D、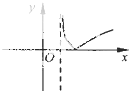 |
已知命题p:π是有理数,q:-π是负数,给出下列四个复合命题:①p或q,②p且q,③非p,④非q,其中真命题是( )
| A、①,② | B、①,③ |
| C、②,③ | D、②,④ |
已知cosθ=
,则cos(π+θ)=( )
| 1 |
| 3 |
A、
| ||||
B、-
| ||||
C、
| ||||
D、-
|