题目内容
 如图是一个圆柱被平面所截后余下部分的三视图,尺寸如图所示,则它的体积为
如图是一个圆柱被平面所截后余下部分的三视图,尺寸如图所示,则它的体积为考点:由三视图求面积、体积
专题:常规题型,空间位置关系与距离
分析:由三视图可知,可看成一个圆柱被平面所截,且体积恰为圆柱的一半.
解答:
解:由三视图可知,
可看成一个圆柱被平面所截,且体积恰为圆柱的一半;
圆柱的底面半径为1,高为4,则V=π×12×4=4π,
则其体积为
×4π=2π.
故答案为:2π.
可看成一个圆柱被平面所截,且体积恰为圆柱的一半;
圆柱的底面半径为1,高为4,则V=π×12×4=4π,
则其体积为
| 1 |
| 2 |
故答案为:2π.
点评:三视图中长对正,高对齐,宽相等;由三视图想象出直观图,一般需从俯视图构建直观图,本题考查了学生的空间想象力,识图能力及计算能力.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
函数f(x)=log2|x-1|的图象大致是( )
A、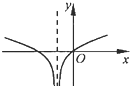 |
B、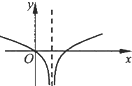 |
C、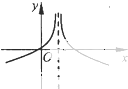 |
D、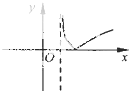 |
已知命题p:π是有理数,q:-π是负数,给出下列四个复合命题:①p或q,②p且q,③非p,④非q,其中真命题是( )
| A、①,② | B、①,③ |
| C、②,③ | D、②,④ |
“a=-2”是“直线a2x+2y+1=0与直线x+ay-2=0互相垂直”的( )
| A、充分不必要条件 |
| B、必要不充分条件 |
| C、充要条件 |
| D、既不充分也不必要条件 |
设集合M={0,1,2},N={1,3},则M∩N是( )
| A、{1} | B、{2} |
| C、{3} | D、{0,1,2,3} |