题目内容
设函数f(x)=(x2-8x+c1)(x2-8x+c2)(x2-8x+c3)(x2-8x+c4),集合M={x|f(x)=0}={x1,x2,…,x7}⊆N*,设c1≥c2≥c3≥c4,则c1-c4= .
考点:二次函数的性质
专题:函数的性质及应用
分析:由已知中集合M={x|f(x)=0}={x1,x2,…,x7}⊆N*,结合函数f(x)的解析式,及韦达定理,我们易求出c1及c4的值,进而得到答案.
解答:
解:由根与系数的关系知xi+yi=8,xi•yi=ci,
这里xi,yi为方程x2-8x+ci=0之根,i=1,…,4.
又∵M={x|f(x)=0}={x1,x2,…,x7}⊆N*,
由集合性质可得(xi,yi)取(1,7),(2,6),(3,4),(4,4),
又c1≥c2≥c3≥c4,
故c1=16,c4=7
∴c1-c4=9
故答案为:9
这里xi,yi为方程x2-8x+ci=0之根,i=1,…,4.
又∵M={x|f(x)=0}={x1,x2,…,x7}⊆N*,
由集合性质可得(xi,yi)取(1,7),(2,6),(3,4),(4,4),
又c1≥c2≥c3≥c4,
故c1=16,c4=7
∴c1-c4=9
故答案为:9
点评:本题考查的知识点是函数与方程的综合运用,其中根据韦达定理,求出c1及c4的值,是解答本题的关键.

练习册系列答案
相关题目
已知三点A(1,1),B(-1,0),C(0,1),若
和
是相反向量,则点D的坐标是( )
| AB |
| CD |
| A、(-2,0) |
| B、(2,2) |
| C、(2,0) |
| D、(-2,-2) |
函数y=x3+
是( )
| 1 |
| x |
| A、奇函数 | B、偶函数 |
| C、既奇又偶函数 | D、非奇非偶函数 |
函数f(x)=log2|x-1|的图象大致是( )
A、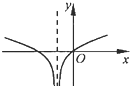 |
B、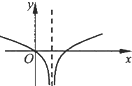 |
C、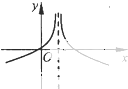 |
D、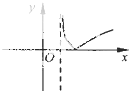 |
“a=-2”是“直线a2x+2y+1=0与直线x+ay-2=0互相垂直”的( )
| A、充分不必要条件 |
| B、必要不充分条件 |
| C、充要条件 |
| D、既不充分也不必要条件 |