题目内容
关于x的不等式0.2(3-2x)<125的解集为( )
A、(-∞,
| ||
B、(
| ||
| C、[-1,+∞) | ||
| D、(-∞,3) |
考点:指、对数不等式的解法
专题:计算题,函数的性质及应用,不等式的解法及应用
分析:化为同底幂的不等式,运用指数函数的单调性,得到一次不等式,解得即可.
解答:
解:不等式0.2(3-2x)<125即为
52x-3<53,
即有2x-3<3,
解得,x<3.
则解集为(-∞,3).
故选D.
52x-3<53,
即有2x-3<3,
解得,x<3.
则解集为(-∞,3).
故选D.
点评:本题考查指数不等式的解法,考查指数函数的单调性的运用,考查运算能力,属于基础题.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
设如图是某几何体的三视图,则该几何体的体积为( )
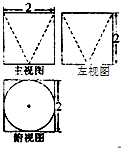

A、
| ||
B、8-
| ||
| C、8-2π | ||
D、8-
|
为了得到函数y=cos(2x+
)的图象,只需把函数y=sin(2x+
)的函数( )
| π |
| 6 |
| π |
| 6 |
A、向左平移
| ||
B、向右平移
| ||
C、向左平移
| ||
D、向右平移
|
下面四个选项大小关系正确的是( )
A、sin
| ||||
B、sin
| ||||
C、cos
| ||||
D、cos
|