设如图是某几何体的三视图.则该几何体的体积为( ) A.2π3B.8-π3C.8-2πD.8-2π3 题目和参考答案——青夏教育精英家教网—

题目内容

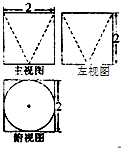
设如图是某几何体的三视图，则该几何体的体积为（　　）

A、

2π

B、8-

C、8-2π

D、8-

2π

考点：由三视图求面积、体积

专题：空间位置关系与距离

分析：由已知可得该几何体是一个正方体挖去一个圆锥得到的组合体，代入体积公式分别计算出正方体和圆锥的体积，相减可得答案．

解答： 解：由已知可得该几何体是一个正方体挖去一个圆锥得到的组合体，
正方体的体积为：2×2×2=8，
圆锥的底面直径为2，故底面半径为1，底面面积为π，高为2，
故圆锥的体积为：

2π

，
故组合体的体积V=8-

2π

，
故选：D

点评：本题考查由三视图求几何体的体积和表面积，根据已知的三视图分析出几何体的形状是关键．

练习册系列答案

设函数f（x）=e^x+e^-x
（1）判断函数f（x）的奇偶性；
（2）证明函数f（x）在（0，+∞）上是单调增函数．

设五个数值31，38，34，35，x的平均数是34，则这组数据的方差是

．

一个容量为M的样本数据，其频率分布表如表．

分组	频数	频率
（10，20]	2	0.10
（20，30]	3
（30，40]	4	0.20
（40，50]
（50，60]	4	0.20
（60，70]	2	0.10
合计		1.00

（Ⅰ）完成频率分布表；
（Ⅱ）画出频率分布直方图；
（Ⅲ）利用频率分布直方图，估计总体的众数、中位数及平均数．

关于x的不等式0.2^（3-2x）＜125的解集为（　　）

已知函数f（x）=ax²+bx，g（x）=lnx．
（1）当a=1，b=2时，求函数y=f （x）-g （x）的图象在点（1，f （1））处的切线方程；
（2）若2a=1-b（b＞1），讨论函数y=f （x）-g （x）的单调性；
（3）若对任意的b∈[-2，-1]，均存在x∈（1，e）使得f （x）＜g （x），求实数a的取值范围．

已知函数f（x）=a^|x+b|（a＞0，a≠1，b∈R）．
（1）若f（x）为偶函数，求b的值；
（2）若f（x）在区间[2，+∞）上是增函数，试求a、b应满足的条件．

试题分类