题目内容
作出y=
+2的函数图象,并求出其单调区间.
| 1 |
| x |
考点:函数单调性的判断与证明
专题:函数的性质及应用
分析:画出函数y=
的图象,通过图象平移,得到函数y=
+2的图象,结合图象得出函数的单调区间.
| 1 |
| x |
| 1 |
| x |
解答:
 解:先画出函数y=
解:先画出函数y=
的图象,
再把函数y=
的图象向上平移2个单位,即可得到函数y=
+2的图象,
如图所示;
结合图象,知;
函数y=
+2在(-∞,0),(0,+∞)是单调减函数.
∴该函数的单调减区间是(-∞,0),(0,+∞).
 解:先画出函数y=
解:先画出函数y=| 1 |
| x |
再把函数y=
| 1 |
| x |
| 1 |
| x |
如图所示;
结合图象,知;
函数y=
| 1 |
| x |
∴该函数的单调减区间是(-∞,0),(0,+∞).
点评:本题考查了函数的图象与应用问题,经过函数图象平移,即可得出函数的图象,结合图象,得出函数的单调性,是基础题.

练习册系列答案
相关题目
双曲线
-y2=-1的离心率为( )
| x2 |
| 2 |
A、
| ||||
B、
| ||||
C、
| ||||
D、
|
△ABC的内角A,B,C的对边分别为a,b,c,若a=10,B=45°,b=7,则△ABC( )
| A、无解 | B、仅有一解 |
| C、仅有两解 | D、无法判断 |
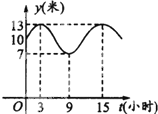 某港口水深y(米)是时间t(0≤t≤24,单位:小时)的函数,下表是水深数据:
某港口水深y(米)是时间t(0≤t≤24,单位:小时)的函数,下表是水深数据: