题目内容
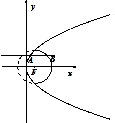 如图所示,直线y=m与抛物线y2=8x交与点A,与圆(x-2)2+y2=16的实线部分交于点B,F为抛物线的焦点,则△ABF的周长的取值范围是( )
如图所示,直线y=m与抛物线y2=8x交与点A,与圆(x-2)2+y2=16的实线部分交于点B,F为抛物线的焦点,则△ABF的周长的取值范围是( )| A、(6,8) |
| B、(4,6) |
| C、(8,12) |
| D、(8,10) |
考点:抛物线的简单性质
专题:计算题,直线与圆,圆锥曲线的定义、性质与方程
分析:由抛物线定义可得|AF|=xA+2,由已知条件推导出△FAB的周长=6+xB,由此能求出三角形ABF的周长的取值范围.
解答:
解:抛物线的准线l:x=-2,焦点F(2,0),
由抛物线定义可得|AF|=xA+2,
∴△FAB的周长=|AF|+|AB|+|BF|=xA+2+(xB-xA)+4=6+xB,
由抛物线y2=8x及圆(x-2)2+y2=16,
得交点的横坐标为2,
∴xB∈(2,6)
∴6+xB∈(8,12)
∴三角形ABF的周长的取值范围是(8,12).
故选:C.

由抛物线定义可得|AF|=xA+2,
∴△FAB的周长=|AF|+|AB|+|BF|=xA+2+(xB-xA)+4=6+xB,
由抛物线y2=8x及圆(x-2)2+y2=16,
得交点的横坐标为2,
∴xB∈(2,6)
∴6+xB∈(8,12)
∴三角形ABF的周长的取值范围是(8,12).
故选:C.
点评:本题考查三角形的周长的取值范围的求法,是中档题,解题时要熟练掌握抛物线的定义和简单性质.

练习册系列答案
相关题目
双曲线
-y2=-1的离心率为( )
| x2 |
| 2 |
A、
| ||||
B、
| ||||
C、
| ||||
D、
|
△ABC的内角A,B,C的对边分别为a,b,c,若a=10,B=45°,b=7,则△ABC( )
| A、无解 | B、仅有一解 |
| C、仅有两解 | D、无法判断 |
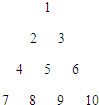 把正整数按上小下大、左小右大的原则排成如图三角形数表(每行比上一行多一个数):设ai,j(i、j∈N*)是位于这个三角形数表中从上往下数第i行、从左往右数第j个数,如a4,2=8,则a51,25为
把正整数按上小下大、左小右大的原则排成如图三角形数表(每行比上一行多一个数):设ai,j(i、j∈N*)是位于这个三角形数表中从上往下数第i行、从左往右数第j个数,如a4,2=8,则a51,25为