Question

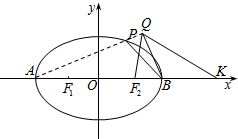
设直线x+y+m=0（m≠0）与曲线E：

x2

a

+

y2

b

=1（a＞0）相交于A，B两点，O是坐标原点，且

OP

=

1

2

（

OA

+

OB

），若直线OP的斜率为-

1

2

，则曲线E的离心率是（　　）

• A、

  2

  2

• B、

  3

  2

• C、

  3

• D、

  6

  2

Answer 1

考点：椭圆的简单性质

专题：圆锥曲线的定义、性质与方程

分析：利用向量的中点公式可知：点P是线段AB的中点，再利用“点差法”和斜率计算公式即可得出a=2b，利用离心率计算公式即可得出．

解答： 解：由

OP

=

1

2

（

OA

+

OB

），可知P为AB的中点，
设P（x₀，y₀），A（x₁，y₁），B（x₂，y₂）
代入曲线方程：bx12+ay12=ab，bx22+ay22=ab，
∴

y1-y2

x1-x2

=-

bx0

ay0

，
∵直线x+y+m=0的斜率为-1，直线OP的斜率为-

1

2

，
∴a=2b，
∵a＞0，∴b＞0，
故曲线E为焦点在x轴上的椭圆，e=

1- b a

=

3

2

．
故选：B．

点评：本题综合考查了椭圆的标准方程及其性质，考查了推理能力和计算能力，属于中档题．