题目内容
直线l过点P(
,2),且与x轴,y轴的正半轴分别交于A,B两点,O为坐标原点.
(1)当△AOB的周长为12时,求直线l的方程;
(2)当△AOB的面积为6时,求直线l的方程.
| 4 |
| 3 |
(1)当△AOB的周长为12时,求直线l的方程;
(2)当△AOB的面积为6时,求直线l的方程.
考点:待定系数法求直线方程
专题:直线与圆
分析:(1)设直线l方程为y=kx+b,k<0.△AOB的周长为12时,建立方程关系,由此能求出直线l的方程.
(2)设直线l方程为y=kx+b,k<0.当△AOB的面积为6时,根据三角形的面积公式,由此能求出直线l的方程.
(2)设直线l方程为y=kx+b,k<0.当△AOB的面积为6时,根据三角形的面积公式,由此能求出直线l的方程.
解答:
解:(1)∵直线l过点P(
,2),且与x,y轴的正方向分别交于A,B两点,
∴设直线l方程为y=kx+b,k<0.
则直线l交x轴的交点为(-
,0),y轴交点为(0,b).
△AOB的周长为12时,
,解得b=3,k=-
,
∴直线l的方程为y=-
x+3.
(2)设直线l方程为y=kx+b,k<0,由(1)知直线l交x轴的交点为(-
,0),y轴交点为(0,b).
当△AOB的面积为6时,
,解得
,或
,
∴直线l的方程为y=-
+3或y=-3x+6.
| 4 |
| 3 |
∴设直线l方程为y=kx+b,k<0.
则直线l交x轴的交点为(-
| b |
| k |
△AOB的周长为12时,
|
| 3 |
| 4 |
∴直线l的方程为y=-
| 3 |
| 4 |
(2)设直线l方程为y=kx+b,k<0,由(1)知直线l交x轴的交点为(-
| b |
| k |
当△AOB的面积为6时,
|
|
|
∴直线l的方程为y=-
| 3 |
| 4 |
点评:本题考查直线方程的求法,根据直线和坐标轴相交求出相应的交点坐标是解决本题的关键.

练习册系列答案
 高效智能课时作业系列答案
高效智能课时作业系列答案
相关题目
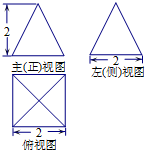
一个空间几何体的三视图如图所示,该几何体的体积为( )

| A、8 | ||
B、
| ||
C、
| ||
| D、6 |
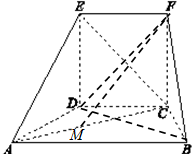 如图,所示的几何体中,四边形CDEF为正方形,四边形ABCD为等腰梯形,AB∥CD,AC=
如图,所示的几何体中,四边形CDEF为正方形,四边形ABCD为等腰梯形,AB∥CD,AC=