题目内容
若A=45°,三边a、b、c成等比数列,求
.
| bsinB |
| c |
考点:正弦定理
专题:计算题,等差数列与等比数列,解三角形
分析:运用等比数列的性质得b2=ac,结合正弦定理,计算即可得到.
解答:
解:三边a、b、c成等比数列即有
b2=ac,
由正弦定理可得,sin2B=sinAsinC,
则
=
=sinA=sin45°=
.
b2=ac,
由正弦定理可得,sin2B=sinAsinC,
则
| bsinB |
| c |
| sinB•sinB |
| sinC |
=sinA=sin45°=
| ||
| 2 |
点评:本题考查正弦定理的运用,考查等比数列的性质,考查运算能力,属于基础题.

练习册系列答案
相关题目
若存在x0∈N+,n∈N+,使f(x0)+f(x0+1)+…+f(x0+n)=63成立,则称(x0,n)为函数f(x)的一个“生成点”.已知函数f(x)=2x+1,x∈N的“生成点”坐标满足二次函数g(x)=ax2+bx+c,则使函数y=g(x)与x轴无交点的a的取值范围是( )
A、0<α<
| ||||||||
B、
| ||||||||
C、α<
| ||||||||
D、0<α<
|
已知函数f(x)的图象是连续不断的一条曲线,且满足 f(1)>0,f(5)<0,若 f(3)>0.则f(x)在下列区间内必有零点的是( )
| A、(1,3) |
| B、(3,5) |
| C、(2,4) |
| D、(3,4) |
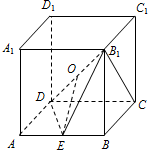 如图,在正方体ABCD-A1B1C1D1中,O,E分别为B1D,AB的中点.
如图,在正方体ABCD-A1B1C1D1中,O,E分别为B1D,AB的中点.