题目内容
已知函数f(x)=|x+1|+2|x-a|,a∈R,
(1)当a=1时,解不等式f(x)>5;
(2)当a>0时,若不等式f(x)>3恒成立,求实数a的取值范围;
(3)当a<0时,若关于x的方程2x[f(x)-1]=a在(1,+∞)上的解集为空集,求实数a的取值范围.
(1)当a=1时,解不等式f(x)>5;
(2)当a>0时,若不等式f(x)>3恒成立,求实数a的取值范围;
(3)当a<0时,若关于x的方程2x[f(x)-1]=a在(1,+∞)上的解集为空集,求实数a的取值范围.
考点:绝对值不等式的解法,函数恒成立问题
专题:计算题,函数的性质及应用,不等式的解法及应用
分析:(1)通过绝对值的含义,去绝对值符号,得到f(x),再解f(x)>5,最后求并集即可;
(2)通过去绝对值,求得f(x)的值域,得到最小值,由最小值大于3,即可;
(3)通过a<0,x>1去掉绝对值,化简方程,分析方程左右两边,即可得到a的范围.
(2)通过去绝对值,求得f(x)的值域,得到最小值,由最小值大于3,即可;
(3)通过a<0,x>1去掉绝对值,化简方程,分析方程左右两边,即可得到a的范围.
解答:
解:(1)f(x)=|x+1|+2|x-1|=
,
由
解得,x<-
;由
解得,x∈∅;
由
解得,x>2.
则不等式的解集为(2,+∞)∪(-∞,-
);
(2)当a>0时,f(x)=
,
当x≤-1时,f(x)≥2a+2,
当-1<x<a时,1+a<f(x)<2+2a;
当x≥a时,f(x)≥1+a.
即有f(x)的值域为[1+a,+∞).
当a>0时,若不等式f(x)>3恒成立,即有
3<1+a,解得,a>2;
(3)当a<0且x>1时,关于x的方程2x[f(x)-1]=a,即为
2x(x+1+2x-2a-1)=a,即为2x(3x-2a)=a,
上式左边大于0,右边小于0,显然方程无解.
则a<0.
|
由
|
| 4 |
| 3 |
|
由
|
则不等式的解集为(2,+∞)∪(-∞,-
| 4 |
| 3 |
(2)当a>0时,f(x)=
|
当x≤-1时,f(x)≥2a+2,
当-1<x<a时,1+a<f(x)<2+2a;
当x≥a时,f(x)≥1+a.
即有f(x)的值域为[1+a,+∞).
当a>0时,若不等式f(x)>3恒成立,即有
3<1+a,解得,a>2;
(3)当a<0且x>1时,关于x的方程2x[f(x)-1]=a,即为
2x(x+1+2x-2a-1)=a,即为2x(3x-2a)=a,
上式左边大于0,右边小于0,显然方程无解.
则a<0.
点评:本题考查绝对值不等式的解法,考查不等式的恒成立问题转化为求函数的最值问题,考查分类讨论的思想方法,属于中档题.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
若存在x0∈N+,n∈N+,使f(x0)+f(x0+1)+…+f(x0+n)=63成立,则称(x0,n)为函数f(x)的一个“生成点”.已知函数f(x)=2x+1,x∈N的“生成点”坐标满足二次函数g(x)=ax2+bx+c,则使函数y=g(x)与x轴无交点的a的取值范围是( )
A、0<α<
| ||||||||
B、
| ||||||||
C、α<
| ||||||||
D、0<α<
|
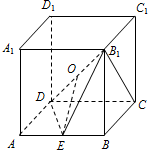 如图,在正方体ABCD-A1B1C1D1中,O,E分别为B1D,AB的中点.
如图,在正方体ABCD-A1B1C1D1中,O,E分别为B1D,AB的中点.