题目内容
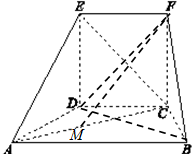 如图,所示的几何体中,四边形CDEF为正方形,四边形ABCD为等腰梯形,AB∥CD,AC=
如图,所示的几何体中,四边形CDEF为正方形,四边形ABCD为等腰梯形,AB∥CD,AC=| 3 |
(1)求证:AC⊥平面FBC
(2)若M为线段AC的中点,求证:EA∥平面FDM.
考点:直线与平面平行的判定,直线与平面垂直的判定
专题:空间位置关系与距离
分析:(1)根据线面垂直的判定定理即可证明AC⊥平面FBC
(2)根据线面平行的判定定理即可证明.
(2)根据线面平行的判定定理即可证明.
解答:
 (1)证明:在△ABC中,
(1)证明:在△ABC中,
因为 AC=
,AB=2,BC=1,
所以 AC⊥BC. …(3分)
又因为 AC⊥FB,BC∩FB=B
所以 AC⊥平面FBC. …(7分)
(2)连结CE,与DF交于点N,连接MN.
因为CDEF为正方形,所以N为CE中点.
在△ACE中,EA∥MN. …(11分)
因为 MN?平面FDM,EA?平面FDM,
所以 EA∥平面FDM. …(15分)
 (1)证明:在△ABC中,
(1)证明:在△ABC中,因为 AC=
| 3 |
所以 AC⊥BC. …(3分)
又因为 AC⊥FB,BC∩FB=B
所以 AC⊥平面FBC. …(7分)
(2)连结CE,与DF交于点N,连接MN.
因为CDEF为正方形,所以N为CE中点.
在△ACE中,EA∥MN. …(11分)
因为 MN?平面FDM,EA?平面FDM,
所以 EA∥平面FDM. …(15分)
点评:本题主要考查空间直线和平面平行和垂直的判定,要求熟练掌握相应的判定定理.

练习册系列答案
 世纪百通期末金卷系列答案
世纪百通期末金卷系列答案
相关题目
若tanα=2,则sin2α值.
| A、1 | ||
B、
| ||
C、
| ||
| D、2 |
将一张坐标纸对折,使点(0,2)与点(-2,0)重合,点(7,3)与点(m,n)重合,则m-n=( )
| A、-8 | B、8 | C、-4 | D、4 |