题目内容
在某次体检中,有6位同学的平均体重为65公斤.用xn表示编号为n(n=1,2,…,6)的同学的体重,且前5位同学的体重如下:
(Ⅰ)求第6位同学的体重x6及这6位同学体重的标准差s;
(Ⅱ)从前5位同学中随机地选2位同学,求恰有1位同学的体重在区间(58,65)中的概率.
| 编号n | 1 | 2 | 3 | 4 | 5 |
| 体重xn | 60 | 66 | 62 | 60 | 62 |
(Ⅱ)从前5位同学中随机地选2位同学,求恰有1位同学的体重在区间(58,65)中的概率.
考点:古典概型及其概率计算公式,极差、方差与标准差
专题:概率与统计
分析:由平均数和标准差的计算公式可得出x6和s,然后由古典概型计算公式可算出所求概率.
解答:
解:(Ⅰ)由题意得
=65 解得x6=80 …(2分)
则6位同学体重的标准差
s=
=7 …(4分)
所以第6位同学的体重x6=80,这6位同学体重的标准差为s=7 …(5分)
(Ⅱ)从前5位同学中任意选出2位同学的基本事件个数有10个,
它们是(601,66),(601,623),(601,604),(601,625),(66,623),(66,604),(66,625),(623,604),(623,625),(604,625)…(8分)
其中恰有1位同学的体重在(58,65)之间的基本事件有4个,
它们是(601,66),(66,623),(66,604),(66,625)…(10分)
所以恰有1位同学的体重在(58,65)之间的概率P=
=
…(12分)
| 60+66+62+60+62+x6 |
| 6 |
则6位同学体重的标准差
s=
|
所以第6位同学的体重x6=80,这6位同学体重的标准差为s=7 …(5分)
(Ⅱ)从前5位同学中任意选出2位同学的基本事件个数有10个,
它们是(601,66),(601,623),(601,604),(601,625),(66,623),(66,604),(66,625),(623,604),(623,625),(604,625)…(8分)
其中恰有1位同学的体重在(58,65)之间的基本事件有4个,
它们是(601,66),(66,623),(66,604),(66,625)…(10分)
所以恰有1位同学的体重在(58,65)之间的概率P=
| 4 |
| 10 |
| 2 |
| 5 |
点评:本题考查统计中的一些数字特征,如平均数和方差,以及古典概型,要对概念有足够的重视.

练习册系列答案
相关题目
函数f(x)的导函数是f′(x),若对任意的x∈R,都有f(x)+2f′(x)<0成立,则( )
A、
| ||||
B、
| ||||
C、
| ||||
| D、无法比较 |
某程序框图如图所示,则该程序运行后输出的值是( )


| A、2 | B、-2 | C、3 | D、-3 |
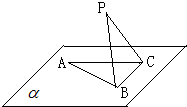 如图,△ABC在平面α内,∠ACB=90°,AB=2BC=2,P为平面α外一个动点,且PC=
如图,△ABC在平面α内,∠ACB=90°,AB=2BC=2,P为平面α外一个动点,且PC= 如图,四边形ABCD是梯形,四边形CDEF是矩形,且平面ABCD⊥平面CDEF,∠BAD=∠CDA=90°,AB=AD=DE=
如图,四边形ABCD是梯形,四边形CDEF是矩形,且平面ABCD⊥平面CDEF,∠BAD=∠CDA=90°,AB=AD=DE=