题目内容
已知一只蚂蚁在圆:x2+y2=1的内部任意随机爬行,若不考虑蚂蚁的大小,则某时刻该蚂蚁爬行在区域|x|+|y|≤1内的概率是( )
A、
| ||
B、
| ||
C、
| ||
D、
|
考点:几何概型
专题:概率与统计
分析:蚂蚁在圆内随机爬行,当该蚂蚁爬行在区域|x|+|y|≤1内时,由图形,算出四边形ABCD的面积,再用这个面积除以圆的面积,即得本题的概率.
解答:
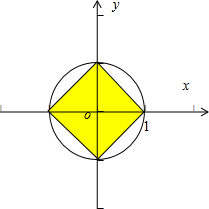 解:一只蚂蚁在圆:x2+y2=1的内部任意随机爬行,
解:一只蚂蚁在圆:x2+y2=1的内部任意随机爬行,
构成全部事件的区域表示的集合为{(x,y)|x2+y2=1},其面积为π
构成事件“某时刻该蚂蚁爬行在区域|x|+|y|≤1内”所表示的集合为{(x,y)||x|+|y|≤1},
如图所示,其面积为
×
=2
则某时刻该蚂蚁爬行在区域|x|+|y|≤1内的概率为P=
=
,
故选:A
 解:一只蚂蚁在圆:x2+y2=1的内部任意随机爬行,
解:一只蚂蚁在圆:x2+y2=1的内部任意随机爬行,构成全部事件的区域表示的集合为{(x,y)|x2+y2=1},其面积为π
构成事件“某时刻该蚂蚁爬行在区域|x|+|y|≤1内”所表示的集合为{(x,y)||x|+|y|≤1},
如图所示,其面积为
| 2 |
| 2 |
则某时刻该蚂蚁爬行在区域|x|+|y|≤1内的概率为P=
| S正方形ABCD |
| S圆 |
| 2 |
| π |
故选:A
点评:本题主要考查几何概型,解题时如需要计算图形的面积,同时考查了分析问题的能力,属于基础题.

练习册系列答案
相关题目
函数f(x)的导函数是f′(x),若对任意的x∈R,都有f(x)+2f′(x)<0成立,则( )
A、
| ||||
B、
| ||||
C、
| ||||
| D、无法比较 |
在花园小区内有一块三边长分别为3米、4米、5米的三角形绿化地,有一只小狗在其内部玩耍,若不考虑小狗的大小,则在任意指定的某时刻,小狗与三角形三个顶点的距离均超过1米的概率是( )
A、1-
| ||
B、1-
| ||
C、2-
| ||
D、2-
|
若[x]表示不超过x的最大整数,如[-2.4]=-3,[3.14]=3,定义函数f(x)=[x[x]],当x∈[0,n)(n∈N*且N≥2)时,设函数f(x)的值域为集合A,记A中的元素个数为an,则
的最小值为( )
| 2an+n+7 |
| n |
A、
| ||
| B、6 | ||
C、
| ||
| D、以上答案都不对 |
已知集合M={x|-1≤x<2},N={x|x-a≤0},若M∩N≠∅,则a的取值范围是( )
| A、(-∞,2] |
| B、(-1,+∞) |
| C、[-1,+∞) |
| D、[-1,1] |
某程序框图如图所示,则该程序运行后输出的值是( )


| A、2 | B、-2 | C、3 | D、-3 |
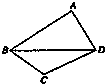 已知一颗粒子的等可能地落入如图所示的四边形ABCD内的任意位置,如果通过大量的实验发现粒子落入△BCD内的频率稳定在
已知一颗粒子的等可能地落入如图所示的四边形ABCD内的任意位置,如果通过大量的实验发现粒子落入△BCD内的频率稳定在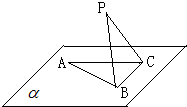 如图,△ABC在平面α内,∠ACB=90°,AB=2BC=2,P为平面α外一个动点,且PC=
如图,△ABC在平面α内,∠ACB=90°,AB=2BC=2,P为平面α外一个动点,且PC=