题目内容
甲乙两种小麦试验品种x年的平均产量如下表：
则根据这组数据估计哪一品种小麦产量较稳定（ ）
| 品种 | 第1年 | 第2年 | 第3年 | 第4年 | 第5年 |
| 甲 | 9.8 | 9.9 | 10.1 | 10 | 10.2 |
| 乙 | 9.4 | 10.3 | 10.8 | 9.7 | 9.8 |
| A、甲乙稳定性相同 | B、乙较稳定 |
| C、甲较稳定 | D、无法比较 |
考点：极差、方差与标准差
专题：概率与统计
分析：根据表中的数据，计算甲、乙的平均数与方差，通过比较即可得出结论．
解答：
解：根据表中的数据，得；
甲的平均值是
=
（9.8+9.9+10.1+10+10.2）=10，
方差是s甲2=
[（9.8-10）2+（9.9-10）2+（10.1-10）2+（10-10）2+（10.2-10）2]=0.02；
乙的平均值是
=
（9.4+10.3+10.8+9.7+9.8）=10，
方差是s乙2=
[（9.4-10）2+（10.3-10）2+（10.8-10）2+（9.7-10）2+（9.8-10）2]=0.244；
∴甲较稳定．
故选：C．
甲的平均值是
. |
| x甲 |
| 1 |
| 5 |
方差是s甲2=
| 1 |
| 5 |
乙的平均值是
. |
| x乙 |
| 1 |
| 5 |
方差是s乙2=
| 1 |
| 5 |
∴甲较稳定．
故选：C．
点评：本题考查了求平均数与方差的问题，解题时应根据公式进行计算即可，是基础题．
练习册系列答案
相关题目
如图，PA垂直于正方形ABCD所在平面，则以下关系错误的是（ ）
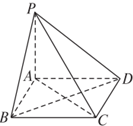
| A、平面PCD⊥平面PAD |
| B、平面PCD⊥平面PBC |
| C、平面PAB⊥平面PBC |
| D、平面PAB⊥平面PAD |
函数f（x）=1-log3x的零点是（ ）
| A、（1，1） | B、1 |
| C、（3，0） | D、3 |
已知函数f（x）=点P（2，1）为圆（x-1）2+y2=25内弦AB的中点，则直线AB的方程为（ ）
| A、x+y-1=0 |
| B、2x+y-3=0 |
| C、x+y-3=0 |
| D、2x-y-5=0 |
在△ABC中，a，b，c分别为角A、B、C的对边，已知∠A=60°，b=1，面积S=
，则
等于（ ）
| 3 |
| a |
| sinA |
A、
| ||||
B、
| ||||
C、
| ||||
D、
|