题目内容
若（1-ax）5的展开式中x3的系数是80，则实数a的值是 ．
考点：二项式定理的应用
专题：二项式定理
分析：根据题意，由二项式定理可得，（ax-1）5的展开式中含x3的项为C53（ax）3•（-1）2=10a3x3=-80x3，结合题意，有10a3=-80，解可得答案．
解答：
解：根据题意，分析可得，
（ax-1）5的展开式中含x3的项为C53（ax）3•（-1）2=10a3x3，
结合题意，有10a3=-80，
解可得a=-2
则实数a的值是-2．
故答案为：-2．
（ax-1）5的展开式中含x3的项为C53（ax）3•（-1）2=10a3x3，
结合题意，有10a3=-80，
解可得a=-2
则实数a的值是-2．
故答案为：-2．
点评：本题考查二项式定理的应用，注意系数与二项式系数的区别．
练习册系列答案
相关题目
甲乙两种小麦试验品种x年的平均产量如下表：
则根据这组数据估计哪一品种小麦产量较稳定（ ）
| 品种 | 第1年 | 第2年 | 第3年 | 第4年 | 第5年 |
| 甲 | 9.8 | 9.9 | 10.1 | 10 | 10.2 |
| 乙 | 9.4 | 10.3 | 10.8 | 9.7 | 9.8 |
| A、甲乙稳定性相同 | B、乙较稳定 |
| C、甲较稳定 | D、无法比较 |
如果一个函数f（x）满足：（1）定义域为x1，x2∈R；（2）任意x1，x2∈R，若x1+x2=0，则f（x1）+f（x2）=0；（3）任意x∈R，若t＞0，总有f（x+t）＞f（x）．则f（x）可以是（ ）
| A、y=-x |
| B、y=x3 |
| C、y=3x |
| D、y=log3x |
设函数f1（x）=x，f2（x）=log2015x，ai=
（i=1，2，3，…，2015），记Ik=|fk（a2）-fk（a1）|+|fk（a3）-fk（a2）|+…+|fk（a2015）-fk（a2014）|，k=1，2，则（ ）
| i |
| 2015 |
| A、I1＜I2 |
| B、I1=I2 |
| C、I2＜I1 |
| D、无法确定 |
已知{an）是等比数列，an＞0，a2a4+2a3a5+a4a6=144，则a3+a5等于（ ）
| A、6 | B、12 | C、18 | D、24 |
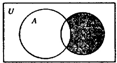设集合U={1，2，3，4，5}，A={1，2，3}，B={2，4}，则图中阴影部分所表示的集合是（ ）| A、{1，3，4} |
| B、{2，4} |
| C、{4，5} |
| D、{4} |