题目内容
函数f(x)=1-log3x的零点是( )
| A、(1,1) | B、1 |
| C、(3,0) | D、3 |
考点:函数零点的判定定理
专题:函数的性质及应用
分析:函数f(x)=1-log3x,根据单调性,解方程1-log3x=0,即可.
解答:
解:∵函数f(x)=1-log3x,
∴函数单调递减,
∵f(x)=1-log3x=0,x=3,
∴函数f(x)=1-log3x的零点有1个,且零点为3,
故选:D
∴函数单调递减,
∵f(x)=1-log3x=0,x=3,
∴函数f(x)=1-log3x的零点有1个,且零点为3,
故选:D
点评:本题考查了函数的性质,零点的概念,属于容易题.

练习册系列答案
 阳光课堂课时作业系列答案
阳光课堂课时作业系列答案
相关题目
甲乙两种小麦试验品种x年的平均产量如下表:
则根据这组数据估计哪一品种小麦产量较稳定( )
| 品种 | 第1年 | 第2年 | 第3年 | 第4年 | 第5年 |
| 甲 | 9.8 | 9.9 | 10.1 | 10 | 10.2 |
| 乙 | 9.4 | 10.3 | 10.8 | 9.7 | 9.8 |
| A、甲乙稳定性相同 | B、乙较稳定 |
| C、甲较稳定 | D、无法比较 |
如果一个函数f(x)满足:(1)定义域为x1,x2∈R;(2)任意x1,x2∈R,若x1+x2=0,则f(x1)+f(x2)=0;(3)任意x∈R,若t>0,总有f(x+t)>f(x).则f(x)可以是( )
| A、y=-x |
| B、y=x3 |
| C、y=3x |
| D、y=log3x |
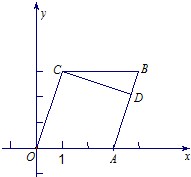 如图,在平行四边形OABC中,点A(3,0),C(1,3),过点C做CD⊥AB于点D.
如图,在平行四边形OABC中,点A(3,0),C(1,3),过点C做CD⊥AB于点D.